
»γΆΦΘ§“―÷Σ≈ΉΈοœΏy=ax²©¹2axΘΪ3(aΓΌ0)Θ§”κx÷αΫΜ”ΎAΓΔBΝΫΒψΘ§”κy÷αΫΜ”ΎΒψCΘ§»τOB=3OAΘ°
Θ®1Θ©«σ≈ΉΈοœΏΒΡΫβΈω ΫΘΜ
Θ®2Θ©Ν§Ϋ”BCΘ§ΒψPΓΔΒψQ «ΒΎ“ΜœσœόΒΡ≈ΉΈοœΏ…œ≤ΜΆ§ΒΡΝΫΒψΘ§ «Ζώ¥φ‘Ύ’β―υΒΡPΒψΘ§ ΙΒΟ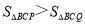 Κψ≥…ΝΔΘΩ»τ¥φ‘ΎΘ§«κ«σPΒψΒΡΉχ±ξΘ§»τ≤Μ¥φ‘ΎΘ§«κΥΒΟςάμ”…ΘΜ
Κψ≥…ΝΔΘΩ»τ¥φ‘ΎΘ§«κ«σPΒψΒΡΉχ±ξΘ§»τ≤Μ¥φ‘ΎΘ§«κΥΒΟςάμ”…ΘΜ
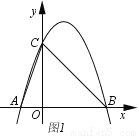
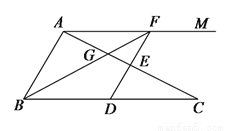
Θ®3Θ©»γΆΦ2Θ§DΈΣ≈ΉΈοœΏΒΡΕ‘≥Τ÷α”κx÷αΒΡΫΜΒψΘ§MΈΣœΏΕΈOC…œ“ΜΒψΘ§ΙΐΒψMΉς÷±œΏlΫΜ≈ΉΈοœΏ”ΎEΓΔFΝΫΒψΘ§Ν§Ϋ”AEΓΔOEΓΔBFΓΔDF»τΓςAEOΓΉΓςDFBΘ§«σMΒψΒΡΉχ±ξΘ°

| ΡξΦΕ | ΗΏ÷–ΩΈ≥Χ | ΡξΦΕ | ≥θ÷–ΩΈ≥Χ |
| ΗΏ“Μ | ΗΏ“ΜΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ | ≥θ“Μ | ≥θ“ΜΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ |
| ΗΏΕΰ | ΗΏΕΰΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ | ≥θΕΰ | ≥θΕΰΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ |
| ΗΏ»ΐ | ΗΏ»ΐΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ | ≥θ»ΐ | ≥θ»ΐΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ |
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚΗ Υύ ΓΕ®Ές –Α≤Ε®«χ2016-2017―ßΡξΑΥΡξΦΕ…œ―ßΤΎΤΎΡ©ΩΦ ‘ ΐ―ß ‘Ψμ Χβ–ΆΘΚΫβ¥πΧβ
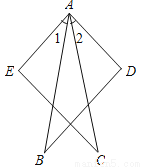
»γΆΦΘ§“―÷ΣABΘΫACΘ§Γœ1ΘΫΓœ2Θ§ΓœBΘΫΓœCΘ§‘ρBDΘΫCEΘ°«κΥΒΟςάμ”…ΘΚ
ΓΨΫβΈωΓΩ
ΓΏΓœ1ΘΫΓœ2
ΓύΓœ1ΘΪΓœBACΘΫΓœ2ΘΪ Θ°
Φ¥ ΘΫΓœDABΘ°
‘ΎΓςABDΚΆΓςACE÷–Θ§
ΓœBΘΫ (“―÷Σ)
ΓΏABΘΫ (“―÷Σ)
ΓœEACΘΫ (“―÷Λ)
ΓύΓςABDΓ’ΓςACE( )
ΓύBDΘΫCE( )
¥πΑΗΦϊΫβΈω ΓΨΫβΈωΓΩ ‘ΧβΖ÷ΈωΘΚΗυΨίΓœ1=Γœ2Θ§Ω…ΒΟΓœ1+ΓœBAC=Γœ2+ΓœBACΘ§ΓœEAC=ΓœDABΘ§»ΜΚσΗυΨί“―÷ΣΧθΦΰΓœB=ΓœCΘ§BD=CEΘ§άϊ”ΟASA÷ΛΟςΓςABDΓ’ΓςACEΘ§»ΜΚσΗυΨί»ΪΒ»»ΐΫ«–ΈΒΡΕ‘”Π±ΏœύΒ»Ω…÷ΛΟςBD=CEΘ° ‘ΧβΫβΈωΘΚΓΏΓœ1=Γœ2 ΓύΓœ1ΘΪΓœBAC=Γœ2ΘΪ ΓœBAC Θ° Φ¥ ΓœEAC =ΓœDABΘ° ‘ΎΓςABDΚΆΓςACE÷–Θ§ ΓœB= ΓœC (“―÷Σ...≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ…ΫΕΪ Γ±θ÷ί –≤Ω2017-2018―ßΡξΑΥΡξΦΕΘ®…œΘ©ΒΎ“Μ¥Έ‘¬ΩΦ ΐ―ß ‘Ψμ Χβ–ΆΘΚΒΞ―ΓΧβ
“―÷ΣΘ§»γΆΦΥυ ΨΘ§AD=ACΘ§BD=BCΘ§OΈΣAB…œ“ΜΒψΘ§Ρ«Ο¥Θ§ΆΦ÷–Ι≤”–Θ®ΓΓΓΓΘ©Ε‘»ΪΒ»»ΐΫ«–ΈΘ°
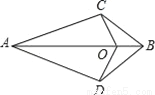
A. 1 B. 2 C. 3 D. 4
C ΓΨΫβΈωΓΩACOΚΆACO, ADBΚΆACB, COBΚΆDOB»ΪΒ».Ι ―ΓC.≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚΙψΈς≥γΉσ –ΧλΒ»œΊ2017Ρξ÷–ΩΦ ΐ―ß“ΜΡΘ ‘Ψμ Χβ–ΆΘΚΧνΩ’Χβ
Ζ÷Ϋβ“ρ ΫΘΚ2a2©¹8=_____Θ°
2Θ®a+2Θ©Θ®a©¹2Θ© ΓΨΫβΈωΓΩ‘≠ Ϋ=.≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚΙψΈς≥γΉσ –ΧλΒ»œΊ2017Ρξ÷–ΩΦ ΐ―ß“ΜΡΘ ‘Ψμ Χβ–ΆΘΚΒΞ―ΓΧβ
œ¬Ν–ΦΗΚΈΧεΒΡ»ΐ ”ΆΦœύΆ§ΒΡ «Θ® Θ©
A. 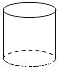 ‘≤÷υ B.
‘≤÷υ B. 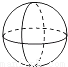 «ρ C.
«ρ C. 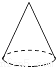 ‘≤ΉΕ D.
‘≤ΉΕ D.  ≥ΛΖΫΧε
≥ΛΖΫΧε
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ…ΫΕΪ Γ2018ΫλΨ≈ΡξΦΕ…œ―ßΤΎΒΎ»ΐ¥Έ‘¬ΩΦ ΐ―ß ‘Ψμ Χβ–ΆΘΚΫβ¥πΧβ
≤ΜΆΗΟςΒΡ¥ϋ÷–ΉΑ”–3Ηω¥σ–ΓœύΆ§ΒΡ–Γ«ρΘ§Τδ÷–ΝΫΗωΈΣΑΉ…ΪΘ§“ΜΗωΈΣΚλ…ΪΘ§ΥφΜζΒΊ¥”¥ϋ÷–Οΰ»Γ“ΜΗω–Γ«ρΚσΖ≈ΜΊΘ§‘ΌΥφΜζΒΊΟΰ»Γ“ΜΗω–Γ«ρΘ§Θ®”ΟΝ–±μΜρ ς–ΈΆΦ«σœ¬Ν– ¬ΦΰΒΡΗ≈¬ Θ©
Θ®1Θ©ΝΫ¥Έ»ΓΒΡ–Γ«ρΕΦ «Κλ«ρΒΡΗ≈¬ ΘΜ
Θ®2Θ©ΝΫ¥Έ»ΓΒΡ–Γ«ρ «“ΜΚλ“ΜΑΉΒΡΗ≈¬ Θ°
Θ®1Θ©ΘΜΘ®2Θ©Θ° ΓΨΫβΈωΓΩ ‘ΧβΖ÷ΈωΘΚΘ®1Θ©”ΟΝ–±μΖ®Ν–ΨΌ≥ωΥυ”–«ιΩωΘ§Ω¥Υυ«σΒΡ«ιΩω”κΉή«ιΩωΒΡ±»÷ΒΦ¥Ω…ΒΟ¥πΑΗΘ§ Θ®2Θ©”…Θ®1Θ©ΒΡΆΦ±μΘ§Ω…ΒΟ“Σ«σΒΡ«ιΩωΘ§”κΉή«ιΩωΉς±»Φ¥Ω…ΒΟ¥πΑΗΘ° ‘ΧβΫβΈωΘΚΘ®1Θ©ΗυΨίΧβ“βΘ§”– ΝΫ¥Έ»ΓΒΡ–Γ«ρΕΦ «Κλ«ρΒΡΗ≈¬ ΈΣΘΜ Θ®2Θ©”…Θ®1Θ©Ω…ΒΟΘ§ΝΫ¥Έ»ΓΒΡ–Γ«ρ «“ΜΚλ“ΜΑΉΒΡ”–4÷÷ΘΜΙ ΤδΗ≈¬ ΈΣΘ°≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ…ΫΕΪ Γ2018ΫλΨ≈ΡξΦΕ…œ―ßΤΎΒΎ»ΐ¥Έ‘¬ΩΦ ΐ―ß ‘Ψμ Χβ–ΆΘΚΒΞ―ΓΧβ
»γΆΦΘ§“―÷ΣΨΊ–ΈABCDΒΡ≥ΛABΈΣ5Θ§ΩμBCΈΣ4Θ§E «BC±Ώ…œΒΡ“ΜΗωΕ·ΒψΘ§AEΓΆEFΘ§EFΫΜCD”ΎΒψFΘ°…ηBE=xΘ§FC=yΘ§‘ρΒψE¥”ΒψB‘ΥΕ·ΒΫΒψC ±Θ§Ρή±μ ΨyΙΊ”ΎxΒΡΚ· ΐΙΊœΒΒΡ¥σ÷¬ΆΦœσ «Θ® Θ©

≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚΚΰΡœ ΓΚβ―τ –2017-2018―ßΡξΑΥΡξΦΕ…œΤΎΡ©ΡΘΡβ ΐ―ß ‘ΨμΘ®Κ§¥πΑΗΘ© Χβ–ΆΘΚΧνΩ’Χβ
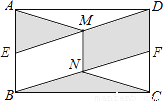
»γΆΦΘ§‘ΎΨΊ–ΈABCD÷–Θ§ΒψEΘ§FΖ÷±π «ABΘ§CDΒΡ÷–ΒψΘ§Ν§ΫαDEΘ§BFΘ§Ζ÷±π»ΓDEΘ§BFΒΡ÷–ΒψMΘ§NΘ§Ν§ΫαAMΘ§CNΘ§MNΘ§»τAB=2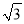 Θ§BC=2
Θ§BC=2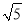 Θ§‘ρΆΦ÷–“θ”Α≤ΩΖ÷ΆΦ–ΈΒΡΟφΜΐΚΆΈΣ________Θ°
Θ§‘ρΆΦ÷–“θ”Α≤ΩΖ÷ΆΦ–ΈΒΡΟφΜΐΚΆΈΣ________Θ°
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ’ψΫ≠ΚΦ÷ίΈςΚΰ«χΒΎ °»ΐ÷–―ß2017-2018―ßΡξΨ≈ΡξΦΕ…œ―ßΤΎΤΎ÷–ΩΦ ‘ ΐ―ß ‘Ψμ Χβ–ΆΘΚΫβ¥πΧβ
»γΆΦΘ§“―÷Σ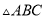 Θ§
Θ§ 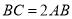 Θ§ΙΐΒψ
Θ§ΙΐΒψ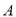 Ής
Ής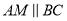 Θ§
Θ§ 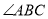 ΤΫΖ÷œΏΖ÷±πΫΜ
ΤΫΖ÷œΏΖ÷±πΫΜ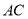 Θ§
Θ§ 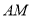 ”ΎΒψ
”ΎΒψ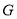 Θ§
Θ§ 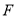 Θ§ΙΐΒψ
Θ§ΙΐΒψ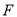 Ής
Ής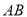 ΒΡΤΫ––œΏΘ§Ζ÷±πΫΜ
ΒΡΤΫ––œΏΘ§Ζ÷±πΫΜ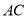 Θ§
Θ§ 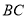 ”ΎΒψ
”ΎΒψ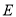 Θ§
Θ§ 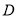 Θ°
Θ°
Θ®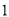 Θ©«σ÷ΛΘΚœΏΕΈ
Θ©«σ÷ΛΘΚœΏΕΈ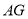 «œΏΕΈ
«œΏΕΈ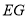 ΚΆ
ΚΆ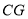 ΒΡ±»άΐ÷–œνΘ°
ΒΡ±»άΐ÷–œνΘ°
Θ®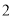 Θ©«σ
Θ©«σ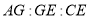 Θ°
Θ°
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΙζΦ ―ß–Θ”≈―Γ - ΝΖœΑ≤αΝ–±μ - ‘ΧβΝ–±μ
Κΰ±± ΓΜΞΝΣΆχΈΞΖ®ΚΆ≤ΜΝΦ–≈œΔΨΌ±®ΤΫΧ® | Άχ…œ”–ΚΠ–≈œΔΨΌ±®Ή®«χ | Βγ–≈’©Τ≠ΨΌ±®Ή®«χ | …φάζ Ζ–ιΈό÷ς“ε”–ΚΠ–≈œΔΨΌ±®Ή®«χ | …φΤσ«÷»®ΨΌ±®Ή®«χ
ΈΞΖ®ΚΆ≤ΜΝΦ–≈œΔΨΌ±®ΒγΜΑΘΚ027-86699610 ΨΌ±®” œδΘΚ58377363@163.com