练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    已知，如图所示，AD=AC，BD=BC，O为AB上一点，那么，图中共有（　　）对全等三角形．

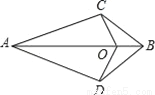
    A. 1 B. 2 C. 3 D. 4

    C 【解析】ACO和ACO, ADB和ACB, COB和DOB全等.故选C.
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源：江苏省盐城市2017-2018学年八年级12月月考数学试卷 题型：解答题

    甲、乙两家体育用品商店出售相同的乒乓球和乒乓球拍，乒乓球每盒定价5元，乒乓球拍每副定价40元．现两家商店都搞促销活动，甲店每买一副球拍赠两盒乒乓球；乙店按九折优惠．某班级需购球拍4副，乒乓球x盒．（x≥8）

    （1）若在甲店购买付款y甲（元），在乙店购买付款y乙（元），分别写出y与x的函数关系式；

    （2）试讨论在哪家商店购买合算？

    （1）y甲=5x+120，y乙=144+4.5x（2）8≤x<48时，在甲商店购买合算，x=48时，在甲乙商店购买一样合算，x>48时，在乙商店购买合算， 【解析】试题分析：本题考查了一次函数的应用及分类讨论的数学思想.(1)直接根据题中甲乙两店的促销方式列式即可;(2)分别根据y甲y乙时列出对应式子求解即可. 【解析】 （1）在甲店购买需付款：y甲=5...

    查看答案和解析>>

    科目：初中数学 来源：甘肃省定西市安定区2016-2017学年八年级上学期期末考试数学试卷 题型：填空题

    在△ABC中，∠C=30°，∠A﹣∠B=30°，则∠A= ．

    90° 【解析】试题分析：根据三角形内角和得到∠A+∠B+∠C=180°，而∠C=30°，则可计算出∠A+∠B+=150°，由于∠A﹣∠B=30°，把两式相加消去∠B即可求得∠A的度数． 【解析】 ∵∠A+∠B+∠C=180°，∠C=30°， ∴∠A+∠B+=150°， ∵∠A﹣∠B=30°， ∴2∠A=180°， ∴∠A=90°． 故答案为90°．

    查看答案和解析>>

    科目：初中数学 来源：山东省滨州市部2017-2018学年八年级（上）第一次月考数学试卷 题型：填空题

    如图，已知点O是△ABC内一点，且点O到三边的距离相等，∠A=40°，则∠BOC=_____．

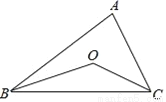
    110°． 【解析】过O作三边的垂线交三边于D,E,F,由题利用HL容易证明RtRtDBO, RtDOCRtEOC,所以∠ABO=∠CBO,∠ACO=∠BCO, ∠A=40°所以∠BCO+∠CBO=70°，∠BOC=110°. 故答案为110°.

    查看答案和解析>>

    科目：初中数学 来源：山东省滨州市部2017-2018学年八年级（上）第一次月考数学试卷 题型：单选题

    如图，在△ABC中，AB=AC，∠A=40°，CD⊥AB于D，则∠DCB等于 ( )

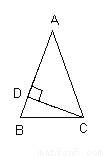
    A、70° B、50° 　 C、40° D、20°

    D 【解析】【解析】 ∵AB=AC，∠A=40°，∴∠B=∠C=（180°-40°）÷2=70°， 又∵CD⊥AB，∴∠BDC=90°，∴∠DCB=90°-70°=20°．故选D．

    查看答案和解析>>

    科目：初中数学 来源：广西崇左市天等县2017年中考数学一模试卷 题型：解答题

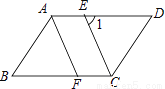
    已知平行四边形ABCD中，CE平分∠BCD且交AD于点E，AF∥CE，且交BC于点F．

    （1）求证：△ABF≌△CDE；

    （2）如图，若∠1=65°，求∠B的大小．

    （1）证明见解析；（2）50°． 【解析】试题分析：（1）由平行四边形的性质得出AB=CD，AD∥BC，∠B=∠D，得出∠1=∠DCE，证出∠AFB=∠1，由AAS证明△ABF≌△CDE即可；（2）由（1）得∠1=∠DCE=65°，由平行四边形的性质和三角形内角和定理即可得出结果． 试题解析：（1）∵四边形ABCD是平行四边形， ∴AB=CD，AD∥BC，∠B=∠D， ∴∠1=∠DCE...

    查看答案和解析>>

    科目：初中数学 来源：广西崇左市天等县2017年中考数学一模试卷 题型：填空题

    如图为二次函数y=ax2+bx+c的图象，在下列说法中：

    ①ac＜0；

    ②方程ax2+bx+c=0的根是x1=﹣1，x2=3；

    ③a+b+c＞0；

    ④当x＞1时，y随着x的增大而增大．

    正确的说法有________．（请写出所有正确的序号）

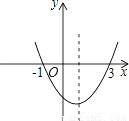
    ①②④ 【解析】（1）由图可知，抛物线开口向上，与y轴交于负半轴， ∴a>0，c<0， ∴ac<0，故①正确； （2）由图可知，抛物线和x轴两交点的横坐标分别为-1和3， ∴方程ax2+bx+c=0的根是x1=﹣1，x2=3，故②正确； （3）由图可知，当时， ，故③错误； （4）由图可知，抛物线和x轴两交点的横坐标分别为-1和3， ∴该抛物线的对称...

    查看答案和解析>>

    科目：初中数学 来源：山东省2018届九年级上学期第三次月考数学试卷 题型：解答题

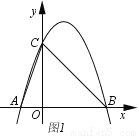
    如图，已知抛物线y=ax²﹣2ax＋3(a≠0)，与x轴交于A、B两点，与y轴交于点C，若OB=3OA．

    （1）求抛物线的解析式；

    （2）连接BC，点P、点Q是第一象限的抛物线上不同的两点，是否存在这样的P点，使得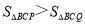恒成立？若存在，请求P点的坐标，若不存在，请说明理由；

    （3）如图2，D为抛物线的对称轴与x轴的交点，M为线段OC上一点，过点M作直线l交抛物线于E、F两点，连接AE、OE、BF、DF若△AEO∽△DFB，求M点的坐标．

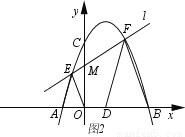
    （1）y=﹣x²＋2x＋3；（2）P；（3）(0， )． 【解析】试题分析：（1）利用韦达定理求二次函数解析式.(2)联立一次函数和二次函数求解.(3)设EF（带k）的函数，与一元二次方程联立，韦达定理,设而不求，利用相似求出k的关系，求出k的值,也就是求出EF函数的表达式，令x=0,求出M坐标. 试题解析： 【解析】 ⑴设A(x1，0)，B(x2，0)， 则x1、x2是...

    查看答案和解析>>

    科目：初中数学 来源：湖南省衡阳市2017-2018学年八年级上期末模拟数学试卷（含答案） 题型：单选题

    如图所示的4×4正方形网格中，∠1+∠2+∠3+∠4+∠5+∠6+∠7=（ ）

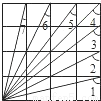
    A．330° B．315° C．310° D．320°

    B． 【解析】 试题解析：由图中可知：①∠4=×90°=45°，②∠1和∠7的余角所在的三角形全等 ∴∠1+∠7=90° 同理∠2+∠6=90°，∠3+∠5=90°，∠4=45° ∴∠1+∠2+∠3+∠4+∠5+∠6+∠7=3×90°+45°=315° 故选B．

    查看答案和解析>>

    同步练习册答案