
已知△ABC中,AD是△ABC的中线,AB=8,AC=6,求AD的取值范围是______.
【解析】【解析】 延长AD至点E,使DE=AD,连接EC,∵BD=CD,DE=AD,∠ADB=∠EDC,∴△ABD≌△ECD,∴CE=AB,∵AB=8,AC=6,CE=8,设AD=x,则AE=2x,∴2<2x<14,∴1<x<7,∴1<AD<7.故答案为:1<AD<7. 发散思维新课堂系列答案
发散思维新课堂系列答案科目:初中数学 来源:北京市分校2017-2018学年度第一学期期中初二数学试卷 题型:单选题
如图,正方形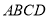 的边长为4,将一个足够大的直角三角板的直角顶点放于点A处,该三角板的两条直角边与
的边长为4,将一个足够大的直角三角板的直角顶点放于点A处,该三角板的两条直角边与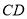 交于点F,与
交于点F,与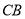 延长线交于点E.四边形
延长线交于点E.四边形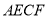 的面积是( ).
的面积是( ).
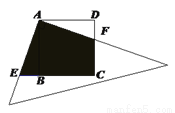
A. 16 B. 12 C. 8 D. 4
A 【解析】试题分析:根据边角边可以证明∆ABE?∆ADF,所以阴影部分的面积是正方形的面积,故阴影部分面积是16,故选A.查看答案和解析>>
科目:初中数学 来源:上海市黄浦区2018届九年级上学期期末调研测试数学试卷(WORD版) 题型:填空题
已知抛物线y=ax2+bx+c开口向上,一条平行于x轴的直线截此抛物线于M、N两点,那么线段MN的长度随直线向上平移而变_____.(填“大”或“小”)
大 【解析】因为二次函数的开口向上,所以点M,N向上平移时,距离对称轴的距离越大,即MN的长度随直线向上平移而变大,故答案为:大.查看答案和解析>>
科目:初中数学 来源:北京市西城外国语学校2017-2018学年度第一学期八年级数学期中试卷 题型:解答题
如图,在△ABC中,AD⊥BC于D, CE平分∠ACB分别交AB、AD于E、F两点,且BD=FD,AB=CF.求证:(1)CE AB;(2)AE=BE.
AB;(2)AE=BE.

查看答案和解析>>
科目:初中数学 来源:北京市西城外国语学校2017-2018学年度第一学期八年级数学期中试卷 题型:解答题
把下列各式因式分解
(1)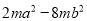 (2)
(2) 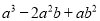 (3)
(3) 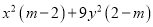
查看答案和解析>>
科目:初中数学 来源:北京市西城外国语学校2017-2018学年度第一学期八年级数学期中试卷 题型:填空题
若分式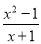 的值为0,则
的值为0,则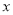 的值等于 .
的值等于 .
查看答案和解析>>
科目:初中数学 来源:北京市西城外国语学校2017-2018学年度第一学期八年级数学期中试卷 题型:单选题
已知:如图,D、E分别在AB、AC上,若AB=AC,AD=AE,∠A =60°,∠B=35°,则∠BDC的度数是( )

A. 95° B. 90° C. 85° D. 80°
A 【解析】【解析】 在△ABE和△ACD中,∵AE=AD,∠A=∠A,AB=AC,∴△ABE≌△ACD(SAS),∴∠C=∠B.∵∠B=35°,∴∠C=35°.∵∠A=60°,∴∠BDC=∠A+∠C=95°,故选A.查看答案和解析>>
科目:初中数学 来源:黑龙江省大庆市2016---2017学年度上期初三数学期末试卷 题型:填空题
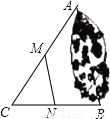
如图,A,B两点被池塘隔开,在A,B外选一点C,连接AC和BC,并分别找出AC和BC的中点M,N,如果测得MM=20m,那么A,B两点间的距离是 .
查看答案和解析>>
科目:初中数学 来源:南京市玄武区2016~2017学年度第一学期期九年级试卷 题型:解答题
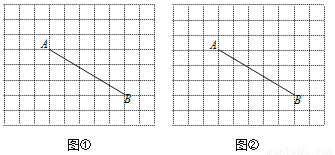
如图,边长为1的小正方形组成了网格,点A、B均是格点,请你仅用无刻度的直尺画出满足下列条件的点P,并在图中标出点P.
(1)图①中,点P在线段AB上且AP=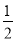 AB;
AB;
(2)图②中,点P在线段AB上且AP=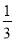 AB.
AB.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com