
a-b=2,a-c=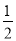 ,则(b-c)3-3(b-c)+
,则(b-c)3-3(b-c)+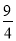 =________.
=________.
科目:初中数学 来源:2018人教版八年级数学下册练习:第二十章达标检测卷 题型:单选题
小明在统计某市6月1日到10日每一天最高气温的变化情况时制作的折线图如图所示,则这10天最高气温的中位数和众数分别是( )
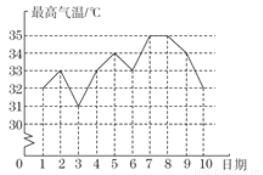
A. 33℃,33℃ B. 33℃,32℃ C. 34℃,33℃ D. 35℃,33℃
A 【解析】某市6月1日到10日每一天最高气温32℃,33℃ ,31℃,33℃,34℃,33℃,35℃,35℃,34℃,32℃,出现次数最多的为33℃,是众数;把这组数据从小到大排列后中间的两个数为33℃,33℃,所以中位数为33℃, 故选A.查看答案和解析>>
科目:初中数学 来源:江苏省苏州市姑苏区2017~2018学年第一学期八年级数学期末考试试卷 题型:解答题
计算:
(1)(﹣a2)3•4a (2)2x(x+1)+(x+1)2.
(1)-4a7; (2) 3x2+4x+1. 【解析】试题分析:(1)根据幂的乘方、同底数幂的乘法进行计算即可; (2)根据单项式乘以多项式以及完全平方公式进行计算即可. 【解析】 (1)原式=﹣a6•4a =﹣4a7; (2)原式=2x2+2x+x2+2x+1 =3x2+4x+1.查看答案和解析>>
科目:初中数学 来源:2018人教版七年级数学下册练习:第八章达标检测卷 题型:解答题
某中学组织学生春游,原计划租用45座客车若干辆,但有15人没有座位;若租用同样数量的60座客车,则多出一辆车,且其余客车恰好坐满,已知45座客车每日每辆租金为220元,60座客车每日每辆租金为300元.试问:
(1)春游学生共多少人?原计划租45座客车多少辆?
(2)若租用同一种车,要使每位同学都有座位,怎样租车更合算?
(1)春游学生共240人,原计划租45座客车5辆;(2)租用4辆60座客车更合算. 【解析】试题分析:(1)首先设租用45座客车x辆,根据题意列出一元一次方程,从而求出x的值,得出答案;(2)根据题意分别求出两种方案的价格,然后进行比较大小,得出答案. 试题解析:(1)设租用45座客车x辆,则租60座客车x-1辆.根据题意,得45x+15=60(x-1) 解得x=5 45x+15...查看答案和解析>>
科目:初中数学 来源:2018人教版七年级数学下册练习:第八章达标检测卷 题型:解答题
解方程组
(1)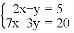
(2)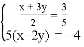
查看答案和解析>>
科目:初中数学 来源:2018人教版七年级数学下册练习:第八章达标检测卷 题型:单选题
如果│x+y-1│和2(2x+y-3)2互为相反数,那么x,y的值为( )
A. 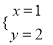 B.
B. 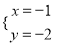 C.
C. 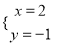 D.
D. 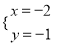
查看答案和解析>>
科目:初中数学 来源:广东省潮州市潮安区2017-2018学年八年级上学期期末教学质量检测数学试卷 题型:解答题
先阅读下面的内容,再解决问题.
例题:若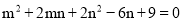 , 求m和n的值
, 求m和n的值
【解析】
∵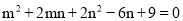
∴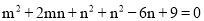
∴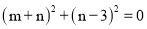
∴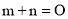 ,
, 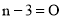
∴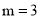 ,
, 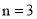
问题:(1)若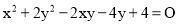 ,求
,求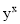 的值.
的值.
(2)已知a,b,c是△ABC的三边长,满足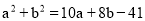 ,且c是△ABC中最长的边,求c的取值范围.
,且c是△ABC中最长的边,求c的取值范围.
查看答案和解析>>
科目:初中数学 来源:广东省潮州市潮安区2017-2018学年八年级上学期期末教学质量检测数学试卷 题型:单选题
下列运用平方差公式计算,错误的是( )
A. 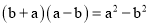 B.
B. 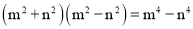
C. 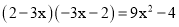 D.
D. 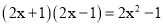
查看答案和解析>>
科目:初中数学 来源:四川省自贡市2016-2017学年上学期九年级期末统一考试数学试卷 题型:填空题
如图,⊙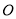 的半径
的半径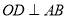 于点
于点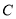 ,连接
,连接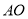 并延长交⊙
并延长交⊙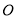 于点
于点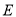 ,连接
,连接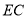 .若
.若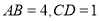 ,则
,则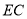 的长为 ___ .
的长为 ___ .

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com