
在平面直角坐标系中,将线段OA向左平移2个单位,平移后,点O、A的对应点分别为点O1、A1.若点O(0,0)A(1,4),则点O1、A1的坐标分别是 ( )
A.(-2,0)(1,4) B.(-2,0)(-1,4)
C.(0,0)(1,4) D.(0,0)(3,4)
B 【解析】 试题分析:向左平移则点的横坐标减去2,则的坐标为(-2,0),的坐标为(-1,4). 备战中考寒假系列答案
备战中考寒假系列答案科目:初中数学 来源:2017年甘肃省白银市中考数学二模试卷 题型:填空题
因式分【解析】
xy2﹣4x=__.
查看答案和解析>>
科目:初中数学 来源:2017-2018学年第一学期期末复习备考之精准复习模拟题八年级浙教版数学试卷(C卷) 题型:填空题
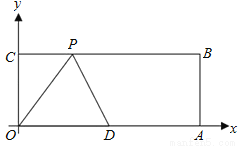
如图,在平面直角坐标系中,矩形OABC的顶点A、C的坐标分别为(10,0),(0,4),点D是OA的中点,点P在BC上运动,当△ODP是腰长为5的等腰三角形时,点P的坐标为______.
查看答案和解析>>
科目:初中数学 来源:2017-2018学年第一学期期末复习备考之精准复习模拟题八年级浙教版数学试卷(A卷) 题型:解答题
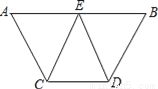
已知:如图,AB∥CD,E是AB的中点,CE=DE.求证:
(1)∠AEC=∠BED;
(2)AC=BD.
查看答案和解析>>
科目:初中数学 来源:2017-2018学年第一学期期末复习备考之精准复习模拟题八年级浙教版数学试卷(A卷) 题型:填空题
函数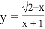 自变量的取值范围为______________
自变量的取值范围为______________
查看答案和解析>>
科目:初中数学 来源:2017-2018学年第一学期期末复习备考之精准复习模拟题八年级浙教版数学试卷(A卷) 题型:单选题
已知点P(-2,1),那么点P关于x轴对称的点P′的坐标是( )
A、(-2,1) B、(-1,2) C、(2,1) D、(-2,-1)
D 【解析】 试题分析:关于x轴对称的点的横坐标相同,纵坐标互为相反数. 点P(-2,1)关于x轴对称的点P′的坐标是(-2,-1),故选D.查看答案和解析>>
科目:初中数学 来源:浙江杭州拱墅区文澜中学2017-2018学年七年级上学期中考试数学试卷(含解析) 题型:解答题
(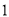 )
)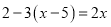 ; (
; (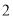 )
)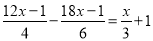 .
.
查看答案和解析>>
科目:初中数学 来源:浙江杭州拱墅区文澜中学2017-2018学年七年级上学期中考试数学试卷(含解析) 题型:单选题
估算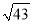 的值最接近于下列哪个整数( ).
的值最接近于下列哪个整数( ).
A. 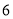 B.
B. 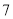 C.
C. 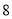 D.
D. 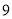
查看答案和解析>>
科目:初中数学 来源:2017-2018学年第一学期期末复习备考之精准复习模拟题八年级人教版数学试卷(C卷) 题型:填空题
如图,△ABC中,BA=BC,∠ABC=40°,∠ABC的平分线与BC的垂直平分线交于点O,E在BC边上,F在AC边上,将∠A沿直线EF翻折,使点A与点O恰好重合,则∠OEF的度数是_____.
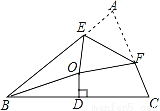
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com