练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    用配方法解关于x的一元二次方程x2﹣2x﹣3=0，配方后的方程可以是（　　）

    A. （x﹣1）2=4 B. （x+1）2=4 C. （x﹣1）2=16 D. （x+1）2=16

    A 【解析】移项，得：x2－2x＝3，配方，得：x2－2x＋1＝3＋1，即(x－1)2＝4.
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源：湖南省邵阳县黄亭市2017~2018学年九年级数学（上）期末综合检测模拟题 题型：解答题

    某中学组织学生到商场参加社会实践活动，他们参与了某种品牌运动鞋的销售工作，已知该运动鞋每双的进价为120元，为寻求合适的销售价格进行了4天的试销，试销情况如表所示：

    （1）观察表中数据，x，y满足什么函数关系？请求出这个函数关系式；

    （2）若商场计划每天的销售利润为3000元，则其单价应定为多少元？

    （1）y是x的反比例函数，；（2）240． 【解析】 试题分析：（1）由表中数据得出xy=6000，即可得出结果； （2）由题意得出方程，解方程即可，注意检验． 试题解析：（1）由表中数据得：xy=6000，∴，∴y是x的反比例函数，故所求函数关系式为； （2）由题意得：（x﹣120）y=3000，把代入得：（x﹣120）•=3000，解得：x=240； 经检验...

    查看答案和解析>>

    科目：初中数学 来源：2017年甘肃省兰州市中考数学模拟试卷 题型：单选题

    某城市2014年底已有绿化面积300公顷，经过两年绿化，绿化面积逐年增加，到2016年底增加到363公顷，设绿化面积平均每年的增长率为x，由题意，所列方程正确的是( )

    A. 300(1＋x)=363 B. 300(1＋x)2=363 C. 300(1＋2x)=363 D. 363(1－x)2=300

    B 【解析】试题分析：知道2004年的绿化面积经过两年变化到2006，绿化面积成为363，设绿化面积平均每年的增长率为x，由题意可列出方程． 【解析】 设绿化面积平均每年的增长率为x， 300（1+x）2=363． 故选B．

    查看答案和解析>>

    科目：初中数学 来源：山东省诸城市2018届九年级上学期期中联考数学试卷（Word版）. 题型：填空题

    若x1，x2是一元二次方程x2﹣2x﹣1=0的两个根，则x12﹣x1+x2的值为_____．

    3

    查看答案和解析>>

    科目：初中数学 来源：山东省诸城市2018届九年级上学期期中联考数学试卷（Word版）. 题型：单选题

    如图，丁轩同学在晚上由路灯AC走向路灯BD，当他走到点P时，发现身后他影子的顶部刚好接触到路灯AC的底部，当他向前再步行20m到达Q点时，发现身前他影子的顶部刚好接触到路灯BD的底部，已知丁轩同学的身高是1.5m，两个路灯的高度都是9m，则两路灯之间的距离是（　 　）

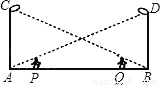
    A. 24m B. 25m C. 28m D. 30m

    D 【解析】由题意可得:EP∥BD,所以△AEP∽△ADB,所以,因为EP=1.5,BD=9,所以,解得:AP=5,因为AP=BQ,PQ=20,所以AB=AP+BQ+PQ=5+5+20=30,故选D.

    查看答案和解析>>

    科目：初中数学 来源：2017年河北省中考数学模拟试卷 题型：解答题

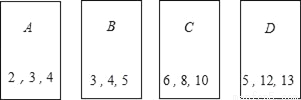
    在四张编号为A，B，C，D的卡片（除编号外，其余完全相同）的正面分别写上如图所示的正整数后，背面向上，洗匀放好．

    （1）我们知道，满足a2+b2=c2的三个正整数a，b，c成为勾股数，嘉嘉从中随机抽取一张，求抽到的卡片上的数是勾股数的概率P1；

    （2）琪琪从中随机抽取一张（不放回），再从剩下的卡片中随机抽取一张（卡片用A，B，C，D表示）．请用列表或画树形图的方法求抽到的两张卡片上的数都是勾股数的概率P2，并指出她与嘉嘉抽到勾股数的可能性一样吗？

    （1）；（2）淇淇与嘉嘉抽到勾股数的可能性不一样． 【解析】试题分析： （1）根据等可能事件的概率的定义，分别确定总的可能性和是勾股数的情况的个数； （2）用列表法列举出所有的情况和两张卡片上的数都是勾股数的情况即可. 试题解析： （1）嘉嘉随机抽取一张卡片共出现4种等可能结果，其中抽到的卡片上的数是勾股数的结果有3种，所以嘉嘉抽取一张卡片上的数是勾股数的概率P1=；...

    查看答案和解析>>

    科目：初中数学 来源：2017年河北省中考数学模拟试卷 题型：填空题

    若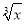=﹣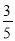，则x=_____；若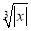=6，则x=_____．

    ﹣ ±216 【解析】因为x的立方等于，所以x=；因为|x|的立方等于6，所以|x|=216，所以x=±216. 故答案为 (1). ﹣ (2). ±216

    查看答案和解析>>

    科目：初中数学 来源：2017年辽宁省营口市大石桥市水源九年一贯制学校中考数学模拟试卷 题型：解答题

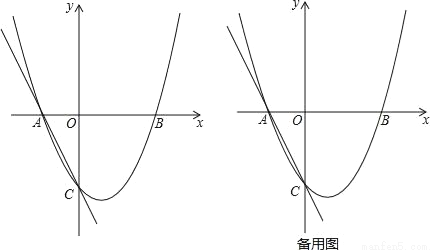
    如图，二次函数y=ax2+bx+c的图象交x轴于A（﹣1，0），B（2，0），交y轴于C（0，﹣2），过A，C画直线．

    （1）求二次函数的解析式；

    （2）点P在x轴正半轴上，且PA=PC，求OP的长；

    （3）点M在二次函数图象上，以M为圆心的圆与直线AC相切，切点为H．

    ①若M在y轴右侧，且△CHM∽△AOC（点C与点A对应），求点M的坐标；

    ②若⊙M的半径为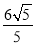，求点M的坐标．

    （1）y=x2﹣x﹣2；（2）；（3）①M（1，﹣2），M′（， ）；②（2，0）或（﹣3，10）． 【解析】（1）根据与x轴的两个交点A、B的坐标，利设出两点法解析式，然后把点C的坐标代入计算求出a的值，即可得到二次函数解析式； （2）设OP=x，然后表示出PC、PA的长度，在Rt△POC中，利用勾股定理列式，然后解方程即可； （3）①根据相似三角形对应角相等可得∠MCH=∠C...

    查看答案和解析>>

    科目：初中数学 来源：山东省2018届九年级上期末复习检测数学试卷 题型：单选题

    二次函数y=ax2+bx+c（a＞0）的顶点为P，其图像与x轴有两个交点A（﹣m，0），B（1，0），交y轴于点C（0，﹣3am+6a），以下说法：

    ①m=3；

    ②当∠APB=120°时，a=；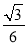

    ③当∠APB=120°时，抛物线上存在点M（M与P不重合），使得△ABM是顶角为120°的等腰三角形；

    ④抛物线上存在点N，当△ABN为直角三角形时，有a≥ ；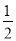

    正确的是（   ）

    A. ①② B. ③④ C. ①②③ D. ①②③④

    D 【解析】试题分析：根据每一种情况分别画出图形，然后根据二次函数的性质得出答案.

    查看答案和解析>>

    同步练习册答案