
如图所示,线段AC的垂直平分线交AB于点D,∠A=43º,则∠BDC的度数为:
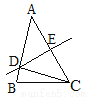
A. 90º B. 60º C. 86º D. 43º
C 【解析】试题解析:∵DE是线段AC的垂直平分线, ∴DA=DC, ∴∠DCA=∠A=43°, ∴∠BDC=∠DCA+∠A=86°, 故选C. 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源:甘肃省武威市2017-2018学年七年级上学期期末考试数学试卷 题型:解答题
一个角的余角比这个角的 少30°,请你计算出这个角的大小.
少30°,请你计算出这个角的大小.
查看答案和解析>>
科目:初中数学 来源:江苏省苏州市2017年中考二模试卷数学试卷 题型:单选题
如图,在菱形ABCD中, AB=6, ∠DAB=60°,AE分别交BC、BD于点E、F,若CE=2 ,连接CF.以下结论:①∠BAF=∠BCF ; ②点E到AB的距离是 2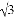 ; ③S△CDF:S△BEF=9:4 ; ④tan∠DCF=3/7 . 其中正确的有( )
; ③S△CDF:S△BEF=9:4 ; ④tan∠DCF=3/7 . 其中正确的有( )
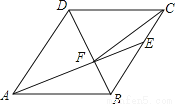
A. 4个 B. 3个 C. 2个 D. 1个
B 【解析】试题分析:∵四边形ABCD是菱形, ∴BA=BC,∠ABD=∠CBD, 在△ABF和△CBF中, , ∴△ABF≌△CBF, ∴∠BAF=∠BCF,①正确; 作EG⊥AB交AB的延长线于G, ∵AD∥BC,∠DAB=60°, ∴∠EBG=60°, EB=BC-CE=4, ∴EG=EB×sin∠EGB=4×=,②正确; ...查看答案和解析>>
科目:初中数学 来源:湖北省襄阳市襄城区2016-2017学年度上学期期末考试八年级数学试卷 题型:解答题
先化简,再求值: 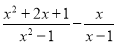 ,其中
,其中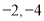
查看答案和解析>>
科目:初中数学 来源:湖北省襄阳市襄城区2016-2017学年度上学期期末考试八年级数学试卷 题型:单选题
把分式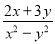 的x,y均扩大为原来的10倍后,则分式的值
的x,y均扩大为原来的10倍后,则分式的值
A. 为原分式值的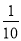 B. 为原分式值的
B. 为原分式值的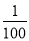
C. 为原分式值的10倍 D. 不变
A 【解析】试题解析:x、y均扩大为原来的10倍后, ∴ 故选A.查看答案和解析>>
科目:初中数学 来源:重庆市秀山县2017-2018学年七年级上学期八校联考数学试卷 题型:解答题
点O为直线AB上一点,在直线AB上侧任作一个∠COD,使得∠COD=90°.
(1)如图1,过点O作射线OE,当OE恰好为∠AOD的角平分线时,请直接写出∠BOD与∠COE之间的倍数关系,即∠BOD= ______ ∠COE(填一个数字);
(2)如图2,过点O作射线OE,当OC恰好为∠AOE的角平分线时,另作射线OF,使得OF平分∠COD,求∠FOB+∠EOC的度数;
(3)在(2)的条件下,若∠EOC=3∠EOF,求∠AOE的度数.
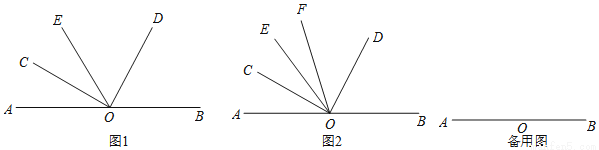
查看答案和解析>>
科目:初中数学 来源:重庆市秀山县2017-2018学年七年级上学期八校联考数学试卷 题型:解答题
计算: 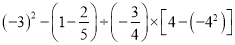 .
.
查看答案和解析>>
科目:初中数学 来源:重庆市秀山县2017-2018学年七年级上学期八校联考数学试卷 题型:单选题
在﹣22,(﹣2)2,﹣(﹣2),﹣|﹣2|中,负数的个数是( )
A. 1个 B. 2个 C. 3个 D. 4个
B 【解析】试题分析:根据有理数的乘方、正数和负数、绝对值的知识对各选项依次计算即可. 【解析】 ﹣22,=﹣4,(﹣2)2=4,﹣(﹣2)=2,﹣|﹣2|=﹣2, ∴是负数的有:﹣4,﹣2. 故选B.查看答案和解析>>
科目:初中数学 来源:2016-2017学年内蒙古鄂尔多斯市鄂托克旗八年级(下)期末数学试卷 题型:填空题
观察下列一系列由火柴棒摆成的图案,第n个图案共需火柴棒 根.
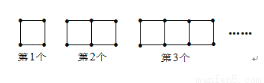
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com