
科目:初中数学 来源:浙江省义乌市四校2017-2018学年八年级上学期第三次作业检测(1月)数学试卷 题型:解答题
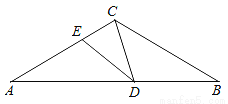
如图,△ABC中,AC=BC,∠ACB=120°,点D在AB边上运动(D不与A、B重合),连结CD.作∠CDE=30°,DE交AC于点E.
(1)当DE∥BC时,△ACD的形状按角分类是 ;
在点D的运动过程中,△ECD的形状可以是等腰三角形吗?若可以,请求出∠AED的度数;若不可以,请说明理由.
查看答案和解析>>
科目:初中数学 来源:内蒙古2017-2018学年八年级上学期期末考试数学试卷 题型:单选题
等腰三角形的一个内角是50°,则另外两个角的度数分别是
A. 65°,65°
B. 50°,80°
C. 65°,65°或50°,80°
D. 50°,50°
C 【解析】试题分析:因为等腰三角形的一个内角是50°,所以当50°的角是顶角时,另外两个底角的度数分别是65°,65°;当50°的角是底角时,另外两个角的度数分别是50°,80°;所以另外两个角的度数分别是65°,65°或50°,80°,故选:C.查看答案和解析>>
科目:初中数学 来源:江苏省南通市2017-2018学年八年级上学期第三次月考数学试卷 题型:填空题
已知实数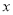 满足
满足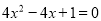 ,则代数式
,则代数式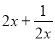 的值为________.
的值为________.
查看答案和解析>>
科目:初中数学 来源:江苏省南通市2017-2018学年八年级上学期第三次月考数学试卷 题型:单选题
甲、乙两人生产某种机器零件,甲每小时比乙多生产5个,甲生产120个所用的时间与乙生产90个所用的时间相等。设甲每小时生产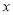 个两件,根据题意,列出的方程是( )
个两件,根据题意,列出的方程是( )
A. 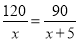 B.
B. 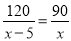 C.
C. 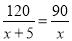 D.
D. 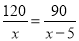
查看答案和解析>>
科目:初中数学 来源:贵州省黔南州2017-2018学年七年级上学期期末联考数学试卷 题型:解答题
有理数a,b,c在数轴上的位置如图所示,且表示数a的点、数b的点到原点的距离相等.

(1)用“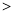 ”“
”“ 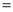 ”“
”“ 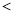 ”填空:b 0,a+b 0,a-c 0,b-c 0;
”填空:b 0,a+b 0,a-c 0,b-c 0;
(2)化简 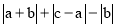 .
.
查看答案和解析>>
科目:初中数学 来源:贵州省黔南州2017-2018学年七年级上学期期末联考数学试卷 题型:填空题
若 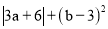 ,则
,则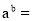 ____.
____.
查看答案和解析>>
科目:初中数学 来源:2017-2018学年西藏拉萨市九年级(上)第一次月考数学试卷 题型:解答题
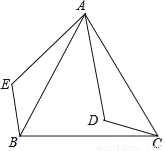
如图,D是等边三角形ABC内一点,将线段AD绕点A顺时针旋转60°,得到线段AE,连接CD,BE.
(1)求证:∠AEB=∠ADC;
(2)连接DE,若∠ADC=105°,求∠BED的度数.
查看答案和解析>>
科目:初中数学 来源:湖北省孝感市八校联谊2017-2018学年八年级数学上册12月联考试卷 题型:单选题
两组邻边分别相等的四边形叫做“筝形”,如图,四边形ABCD是一个筝形,其中AD=CD,AB=CB,在探究筝形的性质时,得到如下结论:①△ABD≌△CBD;②AC⊥BD;③四边形ABCD的面积=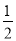 AC•BD,其中正确的结论有( )
AC•BD,其中正确的结论有( )
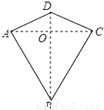
A. ①② B. ①③ C. ②③ D. ①②③
D 【解析】在△BDA和△BDC中, , ∴△BDA≌△BDC, ∴①正确; ∵DA=DC, ∴点D在AC的垂直平分线上, ∵BA=BC, ∴点B在AC的垂直平分线上, ∴BD是AC的垂直平分线, ∴②正确; 四边形ABCD的面积= . ∴③正确. 故选D.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com