
如图,方格纸中小正方形的边长为1,△ABC的三个顶点都在小正方形的格点上,求:
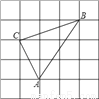
(1) △ABC的面积;
(2)边AC的长;
(3)点B到AC边的距离.
(6分)解(1);(2);(3)h=. 【解析】试题分析:(1)利用三角形所在的正方形面积减三个小直角三角形的面积即可求出; (2)利用勾股定理即可求出AC的长; (3)求出AC,则点B到AC边的距离即为AC边上的高,利用面积公式即可求出. 试题解析:(1)S△ABC=3×3-(×3×1+×2×1+×2×3)=; (2)AC=; (3)设点B到AC边的距离为h,... 云南师大附小一线名师提优作业系列答案
云南师大附小一线名师提优作业系列答案 冲刺100分单元优化练考卷系列答案
冲刺100分单元优化练考卷系列答案科目:初中数学 来源:贵州省六盘水市2018届九年级上学期第二次月考数学试卷 题型:单选题
下列各组线段中是成比例线段的是( )
A. 1cm,2cm,3cm,4cm B. 1cm,2cm,2cm,4cm
C. 3cm,5cm,9cm,13cm D. 1cm,2cm,2cm,3cm
【答案】B
【解析】A选项中,∵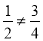 ,∴本选项中这组线段不是成比例线段;
,∴本选项中这组线段不是成比例线段;
B选项中,∵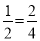 ,∴本选项中的这组线段是成比例线段;
,∴本选项中的这组线段是成比例线段;
C选项中,∵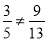 ,∴本选项中的这组线段不是成比例线段;
,∴本选项中的这组线段不是成比例线段;
D选项中,∵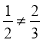 ,∴本选项中的这组线段不是成比例线段;
,∴本选项中的这组线段不是成比例线段;
故选B.
【题型】单选题
【结束】
4
已知3x=4y,则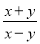 的值为( )
的值为( )
A. 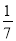 B.
B. 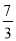 C. 7 D.
C. 7 D. 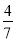
查看答案和解析>>
科目:初中数学 来源:初一数学第一学期5.2.3去分母解一元一次方程 同步练习 题型:单选题
解方程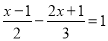 ,去分母正确的是( )
,去分母正确的是( )
A. 3(x-1)-2(2x+1)=6
B. 3(x-1)-2(2x+1)=1
C. 2(x-1)-3(2x+1)=6
D. 3x-1-4x-1=6
A 【解析】解方程中分母的最小公倍数是6,故方程两边同时乘以6得:3(x-1)-2(2x+1)=6. 故选A.查看答案和解析>>
科目:初中数学 来源:安徽省合肥市西校2018届九年级上学期期中考试数学试卷 题型:单选题
若△ABC∽△A′B′C′,相似比为1∶2,则△ABC与△A′B′C′的面积的比为( )
A. 1∶2 B. 2∶1 C. 1∶4 D. 4∶1
C 【解析】试题分析:根据相似三角形面积的比等于相似比的平方计算即可得解.∵△ABC∽△A′B′C′,相似比为1:2,∴△ABC与△A′B′C′的面积的比为1:4. 故选:C.查看答案和解析>>
科目:初中数学 来源:2017-2018学年度鲍沟中学北师大版八年级数学上册 第一章 勾股定理 检测题 题型:解答题
如图,在梯形ABCD中,  利用面积法证明勾股定理.
利用面积法证明勾股定理.
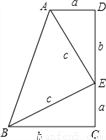
查看答案和解析>>
科目:初中数学 来源:2017-2018学年度鲍沟中学北师大版八年级数学上册 第一章 勾股定理 检测题 题型:单选题
如图,所有三角形都是直角三角形,所有四边形都是正方形,已知S1=4,S2=9,S3=8,S4=10,则S=( )
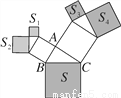
A. 25 B. 31 C. 32 D. 40
B 【解析】试题分析:如图,分别求出AB2、AC2,进而得到BC2,即可解决问题. 【解析】 如图,由题意得: AB2=S1+S2=13, AC2=S3+S4=18, ∴BC2=AB2+AC2=31, ∴S=BC2=31, 故选B.查看答案和解析>>
科目:初中数学 来源:北师大版九年级上册4.7三角形相似专题--高的比等于相似比 题型:解答题
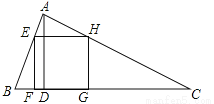
(2016湖南省怀化市)如图,△ABC为锐角三角形,AD是BC边上的高,正方形EFGH的一边FG在BC上,顶点E、H分别在AB、AC上,已知BC=40cm,AD=30cm.
(1)求证:△AEH∽△ABC;
(2)求这个正方形的边长与面积.
查看答案和解析>>
科目:初中数学 来源:人教版九年级上册数学 第24章小结与复习 练习 题型:填空题
如图,⊙O的半径是2,直线l与⊙O相交于A、B两点,M、N是⊙O上的两个动点,且在直线l的异侧,若∠AMB=45°,则四边形MANB面积的最大值是__.
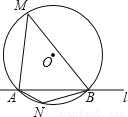
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com