练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

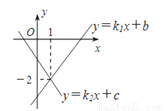
    直线l1：y=k1x+b与直线l2：y=k2x+c在同一平面直角坐标系中的图象如图所示，则关于x的不等式k1x+b＜k2x+c的解集为________ 

    x＜1 【解析】根据一次函数与不等式的关系可得: k1x+b＜k2x+c表示直线l1在直线l2的下方,所以根据图象可得: x＜1,故答案为: x＜1.
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源：江西省2017年秋人教七年级数学上册期末模拟卷 题型：单选题

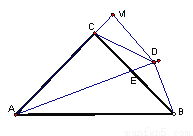
    如图，在△ABC中，AC=BC，∠ACB=900，AE平分∠BAC交BC于E，BD⊥AE于D，DM⊥AC交AC的延长线于M，连接CD。下列结论：

    ①AC+CE=AB；②CD= 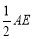，③∠CDA=450 ，④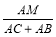为定值。

    其中正确的结论有（　　）

    A.1个 B.2个 C.3个 D.4个

    D 【解析】过E作EQ⊥AB于Q，作∠ACN=∠BCD，交AD于N，过D作DH⊥AB于H，根据角平分线性质求出CE=EQ，DM=DH，根据勾股定理求出AC=AQ，AM=AH，根据等腰三角形的性质和判定求出BQ=QE，即可求出①；根据三角形外角性质求出∠CND=45°，证△ACN≌△BCD，推出CD=CN，即可求出②③；证△DCM≌△DBH，得到CM=BH，AM=AH，即可求出④． ...

    查看答案和解析>>

    科目：初中数学 来源：山东省潍坊高新技术产业开发区2017-2018学年八年级上期末模拟数学试卷 题型：解答题

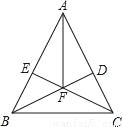
    如图，在△ABC中，AB=AC，BD⊥AC于D，CE⊥AB于E，BD、CE相交于F．

    求证：AF平分∠BAC．

    证明见解析. 【解析】试题分析：先根据AB=AC，可得∠ABC=∠ACB，再由垂直，可得90°的角，在△BCE和△BCD中，利用内角和为180°，可分别求∠BCE和∠DBC，利用等量减等量差相等，可得FB=FC，再易证△ABF≌△ACF，从而证出AF平分∠BAC． 试题解析：证明：∵AB=AC(已知)， ∴∠ABC=∠ACB(等边对等角). ∵BD、CE分别是高， ∴...

    查看答案和解析>>

    科目：初中数学 来源：山东省潍坊高新技术产业开发区2017-2018学年八年级上期末模拟数学试卷 题型：填空题

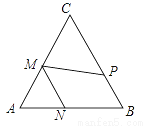
    如图，在等边△ABC中，AB=4，P、M、N分别是BC、CA、AB边上动点，则PM+MN的最小值是________．

    【解析】作点B关于直线AC的对称点K，连接AK、CK，作点N关于直线AC的对称点N′，作N′P′⊥BC于P′，交AC于M′，则线段N′P′的长即为PM+MN的最小值（垂线段最短）． ∵△ABC是等边三角形，易知，四边形ABCK是菱形， N′P′是菱形的高=4×=2 ， 则PM+MN的最小值是2， 故答案是：2．

    查看答案和解析>>

    科目：初中数学 来源：山东省聊城市莘县2017-2018学年八年级（上）期末模拟数学试卷（含答案） 题型：解答题

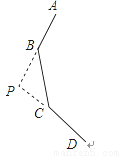
    如图为一个正n边形的一部分，AB和DC延长后相交于点P，若∠BPC=120°，求n．

    n=12． 【解析】试题分析:因为是正多边形,所以外角相等,根据∠BPC=120°,利用三角形内角和可求出正多边形的外角,再利用多边形外角等于360°,即可求出正多边形的边数. 试题解析:∵PB=PC,∠BPC=120°, ∴∠PBC=∠PCB=（180°﹣∠BPC）=30°, 即正n边形的一个外角为30°, ∴n==12．

    查看答案和解析>>

    科目：初中数学 来源：山东省聊城市莘县2017-2018学年八年级（上）期末模拟数学试卷（含答案） 题型：填空题

    如果两个直角三角形，满足斜边和一条直角边相等，那么这两个直角三角形 ________（填“是”或“不是”）全等三角形．

    是 【解析】因为在两个直角三角形中,斜边和任意一条直角边对应相等,则这两个直角三角形全等,故答案为:能.

    查看答案和解析>>

    科目：初中数学 来源：山东省聊城市莘县2017-2018学年八年级（上）期末模拟数学试卷（含答案） 题型：单选题

    已知等腰△ABC中，AD⊥BC于点D，且AD=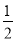BC，则△ABC底角的度数为（ ）

    A、45°或75° B、75°

    C、45°或75°或15° D、60°

    C． 【解析】 试题分析：分三种情况讨论，①如图1，当AB=AC时， ∵AD⊥BC， ∴BD=CD， ∵AD=BC， ∴AD=BD=CD， ∴底角为45°； ②如图2，当AB=BC时， ∵AD=BC， ∴AD=AB， ∴∠ABD=30°， ∴∠BAC=∠BCA=75°， ∴底角为75°． ③如图3，当AB=BC时，...

    查看答案和解析>>

    科目：初中数学 来源：浙江省杭州市2017-2018学年八年级上学期期中考试数学试卷（含解析） 题型：解答题

    某房地产开发公司计划建A、B两种户型的住房共80套，该公司所筹资金不少于2090万元，但不超过2096万元，且所筹资金全部用于建房，两种户型的建房成本和售价如下表：

    A

    B

    成本(万元/套)

    25

    28

    售价(万元/套)

    30

    34

    （1）该公司对这两种户型住房有哪几种建房方案？

    （2）该公司如何建房获得利润最大？

    （3）根据市场调查，每套B型住房的售价不会改变，每套A型住房的售价将会提高a万元(a>0)，且所建的两种住房可全部售出，该公司又将如何建房获得利润最大？

    （注：利润=售价-成本）

    （1）三种建房方案（2）A型住房48套，B型住房32套获得利润最大（3）当O<a<l时， x=48，W最大，当a=l时，a-1=O，三种建房方案获得利润相等，当a>1时，x=50，W最大. 【解析】（1）根据“该公司所筹资金不少于2090万元，但不超过2096万元”，列出不等式进行求解，确定建房方案； （2）根据：利润=售价-成本，利润就可以写成关于x的函数，根据函数...

    查看答案和解析>>

    科目：初中数学 来源：重庆市2017-2018学年七年级（上）期中数学试卷 题型：单选题

    下列说法错误的有( )

    ①单项式－2πab的次数是3次；
    ②－m表示负数；

    ③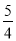是单项式；
    ④m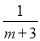＋是多项式．

    A. 4个 B. 3个 C. 2个 D. 1个

    B 【解析】试题解析：①单项式的次数是次.故错误. ②可以表示正数，负数，零.故错误. ③是单项式.正确. ④不是多项式.故错误. 错误的有个. 故选B.

    查看答案和解析>>

    同步练习册答案