练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

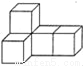
    如图是由五个大小相同的正方体搭成的几何体，从_____面看所得到的图形面积最小．

    左 【解析】从正面看第一层是三个小正方形，第二层左边一个小正方形，共四个小正方形； 从上面看第一层左边一个小正方形，第二层是三个小正方形，共四个小正方形； 从左面看第一层两个小正方形，第二层左边一个小正方形，共三个小正方形; 故答案为：左.
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源：黄金30题系列 九年级数学 大题好拿分 题型：解答题

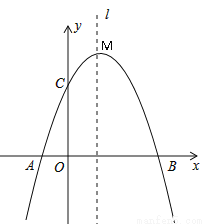
    已知：抛物线y=ax2+bx+c经过A（-1，0）、B（3，0）、C（0，3）三点，直线l是抛物线的对称轴，M为它的顶点

    （1）求抛物线的函数关系式；

    （2）求△MCB的面积；

    （3）设点P是直线l上的一个动点，当PA+PC最小时，求最小值．

    （1）抛物线的函数关系式为y=-x2+2x+3；（2）3；（3） 【解析】试题分析：（1）根据待定系数法求出抛物线解析式； （2）先求出直线BC与对称轴的交点，即可得出MN，再用面积之和即可得出结论； （3）先根据抛物线的对称性，判断出点P是直线BC与抛物线的对称轴l的交点，根据（2）直接得出点P坐标． 试题解析：（1）∵抛物线y=ax2+bx+c经过A（-1，0）、B（...

    查看答案和解析>>

    科目：初中数学 来源：2017年广西防城港市中考数学模拟试卷 题型：填空题

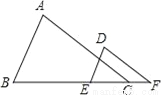
    如图，已知∠A=∠D，要使△ABC∽△DEF，还需添加一个条件，你添加的条件是__．（只需写一个条件，不添加辅助线和字母）

    AB∥DE（答案不唯一）． 【解析】在△ABC和△DEF中，已经有一个条件：∠A=∠D，根据三角形相似的判定方法中的：（1）有两个角对应相等的两个三角形相似；（2）有两边对应成比例，且夹角相等的两个三角形相似；可知：只需再添加“一对对应角相等”或“夹∠A、∠D的两边成比例”即可得到：△ABC∽△DEF，因此本题的答案不是唯一的，如添加的一个条件可以是：①∠B=∠DEF或②∠ACB=∠F或③A...

    查看答案和解析>>

    科目：初中数学 来源：黄金30题系列 九年级数学 小题好拿分 题型：填空题

    圆心角为120°的扇形的半径为3，则这个扇形的面积为 （结果保留）．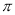

    【解析】试题分析：此题考查扇形面积的计算，熟记扇形面积公式，即可求解. 根据扇形面积公式，计算这个扇形的面积为.

    查看答案和解析>>

    科目：初中数学 来源：黄金30题系列 九年级数学 小题好拿分 题型：填空题

    若方程是关于x的一元二次方程，则m= .

    0 【解析】此题考查一元二次方程的概念 答案 -1

    查看答案和解析>>

    科目：初中数学 来源：黄金30题系列 九年级数学 小题好拿分 题型：单选题

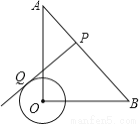
    在Rt△AOB中，OA=OB=3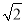，⊙O的半径为1，点P是AB边上的动点，过点P作⊙O的一条切线PQ（点Q为切点），则切线PQ的最小值为（ ）．

    A．2 B．3 C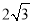． D．2

    D． 【解析】 试题解析：连接OP、OQ． ∵PQ是⊙O的切线， ∴OQ⊥PQ； 根据勾股定理知PQ2=OP2-OQ2， ∴当PO⊥AB时，线段PQ最短， ∵在Rt△AOB中，OA=OB=3， ∴AB=OA=6， ∴OP==3， ∴PQ==2． 故选D．

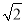
    查看答案和解析>>

    科目：初中数学 来源：黄金30题系列 九年级数学 小题好拿分 题型：单选题

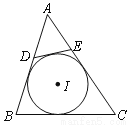
    如图，⊙I为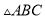的内切圆，点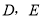分别为边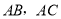上的点，且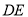为⊙I的切线，若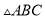的周长为21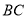， 边的长为6，则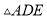的周长为（　　）

    A. 15 B. 8 C. 9 D. 7.5

    C 【解析】试题分析：∵BG和BF是圆的切线， ∴BF=BG， 同理，DG=DI，EH=EI，CF=CH． ∴BG+CH=BC=6， △ADE的周长=AD+AE+DE=AD+AE+DI+IE=AD+AE+DG+EH=AG+AH=21-6-6=9．故选C．

    查看答案和解析>>

    科目：初中数学 来源：安徽省芜湖市教育集团2017-2018学年度上学期八年级第二次月考 题型：填空题

    点A（2，－3）关于x轴的对称点A′的坐标是__________；

    (2, 3) 【解析】试题分析：两点关于x轴对称，则两点的横坐标相等，纵坐标互为相反数．

    查看答案和解析>>

    科目：初中数学 来源：2018年春人教版八年级数学下册（广西）期中测试 题型：解答题

    如图，在Rt△ABC中，∠ACB＝90°，CD⊥AB于D，AC＝20，BC＝15.求AB和CD的长．

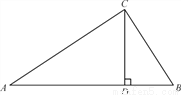
    AB＝25，CD＝12. 【解析】试题分析：根据勾股定理AB=，代入计算即可；根据三角形的面积公式，代入计算即可求出CD的长． 试题解析： （1）在Rt△ABC中， ∵在Rt△ABC中，∠ACB=90°，BC=15，AC=20， ∴AB===25； ∴AB的长是25； （2）∵S△ABC=AC•BC=AB•CD， ∴AC•BC=AB•CD ∴20×15=25CD， ...

    查看答案和解析>>

    同步练习册答案