
如图,为抄近路践踏草坪是一种不文明的现象,请你用数学知识解释出这一现象的原因 .

 数学奥赛暑假天天练南京大学出版社系列答案
数学奥赛暑假天天练南京大学出版社系列答案科目:初中数学 来源:北师大版数学七年级上册 第四章 基本平面图形练习题 题型:解答题
按要求作图:如图,在同一平面内有四个点A、B、C、D.
①画射线CD;②画直线AD;③连结AB;④直线BD与直线AC相交于点O.
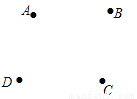
查看答案和解析>>
科目:初中数学 来源:北师大版数学七年级上册 第四章 基本平面图形练习题 题型:单选题
如图,军舰从港口沿OB方向航行,它的方向是( )
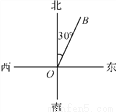
A. 东偏南30° B. 南偏东30° C. 南偏西30° D. 北偏东30°
D 【解析】【解析】 军舰从港口沿OB方向航行,它的方向是北偏东30°.故选D.查看答案和解析>>
科目:初中数学 来源:北师大版数学七年级上册 第四章 基本平面图形练习题 题型:解答题
已知线段a、b(a>b),用尺规作图法作一条线段,使其等于2a-b(不写作法,保留作图痕迹).

查看答案和解析>>
科目:初中数学 来源:北师大版数学七年级上册 第四章 基本平面图形练习题 题型:单选题
(2012•葫芦岛)如图,C是线段AB上一点,M是线段AC的中点,若AB=8cm,BC=2cm,则MC的长是( )

A. 2 cm B. 3 cm C. 4 cm D. 6 cm
B 【解析】试题分析:由图形可知AC=AB﹣BC,依此求出AC的长,再根据中点的定义可得MC的长. 【解析】 由图形可知AC=AB﹣BC=8﹣2=6cm, ∵M是线段AC的中点, ∴MC=AC=3cm. 故MC的长为3cm. 故选B.查看答案和解析>>
科目:初中数学 来源:北师大版数学七年级上册 第四章 基本平面图形练习题 题型:解答题
李明乘车回奶奶家,发现这条汽车线路上共有6个站(包括始发站和终点站),学习本节知识后,善于思考的小明已猜到这条线路上有多少种不同的票价,还要准备多少种不同的车票,聪明的你想到了吗?
15 30 【解析】试题分析:票价只需要考虑有多小条线段即可,车票要考虑起点和终点. 试题解析:【解析】 有15种不同票价,有30种不同车票.查看答案和解析>>
科目:初中数学 来源:北师大版数学七年级上册 第四章 基本平面图形练习题 题型:单选题
小红家分了一套住房,她想在自己的房间的墙上钉一根细木条,挂上自己喜欢的装饰物,那么小红至少需要几根钉子使细木条固定( )
A. 1根 B. 2根 C. 3根 D. 4根
B 【解析】试题分析:根据两点确定一条直线这一基本事实即可解答. 【解析】 因为两点就可确定一条直线,所以需要两根钉子来固定. 故选B.查看答案和解析>>
科目:初中数学 来源:2018年春人教版七年级数学下册期中测试 题型:解答题
如图,在四边形ABCD中,延长AD至E,已知AC平分∠DAB,∠DAB=70°,∠1=35°.
(1)求证:AB∥CD;
(2)求∠2的度数.
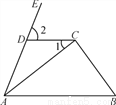
查看答案和解析>>
科目:初中数学 来源:山东省诸城市2018届九年级上期末模拟数试卷 题型:单选题
如图,把矩形纸片ABCD沿EF翻折,点A恰好落在BC边的A′处,若AB= 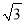 ,∠EFA=60°,则四边形A′B′EF的周长是( )
,∠EFA=60°,则四边形A′B′EF的周长是( )
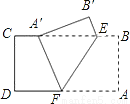
A. 1+3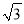 B. 3+
B. 3+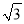 C. 4+
C. 4+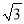 D. 5+
D. 5+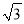
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com