
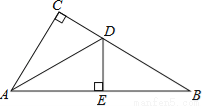
如图,在△ABC中,∠C=90°,∠B=30°,AD是△ABC的角平分线,DE⊥AB,垂足为E,DE=1,则BC=( )
A. 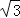 B. 2 C. 3 D.
B. 2 C. 3 D. 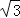 +2
+2
科目:初中数学 来源:北师大版数学八年级上册期中测评 题型:解答题
当a=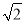 -1时,求2(a+
-1时,求2(a+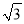 )(a-
)(a-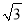 )-a(a-6)+6的值.
)-a(a-6)+6的值.
查看答案和解析>>
科目:初中数学 来源:山东省无棣县2017-2018学年八年级上学期期中考试数学试卷. 题型:解答题
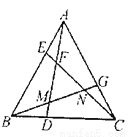
如图,已知△ABC是等边三角形,E,D,G分别在AB,BC,AC边上,且AE=BD=CG,连接AD,BG,CE,相交于F,M,N.
(1)求证:AD=CE;
(2)求∠DFC的度数:
(3)试判断△FMN的形状,并说明理由.
查看答案和解析>>
科目:初中数学 来源:山东省无棣县2017-2018学年八年级上学期期中考试数学试卷. 题型:填空题
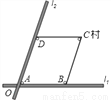
如图,两条笔直的公路 ,
,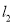 相交于点O,村庄C的村民在公路的旁边建三个加工厂A,B,D,已知AB=BC=CD=DA=5公里,村庄C到公路
相交于点O,村庄C的村民在公路的旁边建三个加工厂A,B,D,已知AB=BC=CD=DA=5公里,村庄C到公路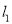 的距离为4公里,则村庄C到公路
的距离为4公里,则村庄C到公路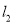 的距离是_____公里.
的距离是_____公里.
查看答案和解析>>
科目:初中数学 来源:山东省无棣县2017-2018学年八年级上学期期中考试数学试卷. 题型:单选题
下列从左边到右边的变形,是因式分解的是( )
A. 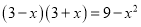 B.
B. 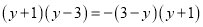
C. 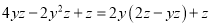 D.
D. 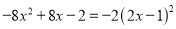
查看答案和解析>>
科目:初中数学 来源:北京四中2017-2018学年上学期初中八年级期中考试数学试卷 题型:解答题
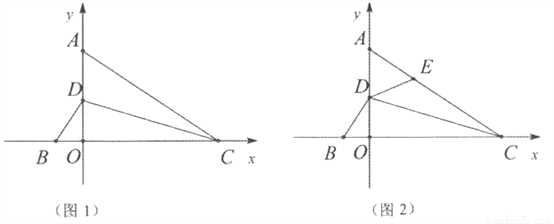
如图1,点A、D在y轴正半轴上,点B、C分别在x轴上,CD平分∠ACB,与y轴交于D点,∠CAO=90°-∠BDO.
(1)求证:AC=BC:
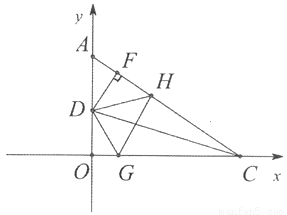
(2)如图2,点C的坐标为(4,0),点E为AC上一点,且∠DEA=∠DBO,求BC+EC的长;
(3)如图3,过D作DF⊥AC于F点,点H为FC上一动点,点G为OC上一动点,当H在FC上移动、点G在OC上移动时,始终满足∠GDH=∠GDO+∠FDH,试判断FH、GH、OG这三者之间的数量关系,写出你的结论并加以证明.
 (图3)
(图3)
查看答案和解析>>
科目:初中数学 来源:北京四中2017-2018学年上学期初中八年级期中考试数学试卷 题型:填空题
若a2+b2-2a-6b+10=0,则a+b=___________.
4 【解析】由a²+b²?2a-6b+10=0, 得a²?2a+1+b²-6b+9=0, 即(a?1) ²+(b-3) ²=0 ∵(a?1) ²?0,(b-3) ²?0 ∴a?1=0,b-3=0 即a=1,b=3 ∴a+b=1+3=4. 故答案为:4.查看答案和解析>>
科目:初中数学 来源:天津市宝坻区口东镇2018届九年级12月月考数学试卷 题型:解答题
某水果批发商销售每箱进价为40元的苹果,物价部门规定每箱售价不得高于55元,市场调查发现,若每箱以50元的价格销售,平均每天销售90箱,价格每提高1元,平均每天少销售3箱.
(1)求平均每天销售量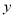 箱与销售价
箱与销售价 元/箱之间的函数关系式.
元/箱之间的函数关系式.
(2)当每箱苹果的销售价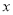 为多少元时,可以使获得的销售利润w最大?最大利润是多少?
为多少元时,可以使获得的销售利润w最大?最大利润是多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com