
下列从左边到右边的变形,是因式分解的是( )
A. 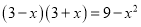 B.
B. 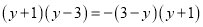
C. 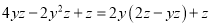 D.
D. 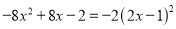
 浙江名校名师金卷系列答案
浙江名校名师金卷系列答案科目:初中数学 来源:山东省邹城市2017-2018学年七年级第一学期数学第二次月考试卷 题型:单选题
下列运用等式的性质,变形不正确的是( )
A. 若x=y,则x+5=y+5 B. 若a=b则ac=bc
C. 若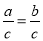 ,则a=b D. 若x=y,则
,则a=b D. 若x=y,则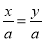
查看答案和解析>>
科目:初中数学 来源:北师大版数学八年级上册期中测评 题型:填空题
已知一个直角三角形的两边长分别为3和4,则第三边长是__________
5或 【解析】试题分析:分两种情况(1)3和4都是直角边,由勾股定理求得斜边为5;(2)3是直角边,4是斜边,由勾股定理求得另一条直角边为.查看答案和解析>>
科目:初中数学 来源:山东省无棣县2017-2018学年八年级上学期期中考试数学试卷. 题型:解答题
计算:(1)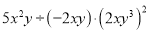
(2)下面是小颖化简整式的过程,仔细阅读后解答所提出的问题。
【解析】
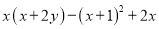
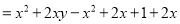 第一步
第一步
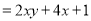 第二步
第二步
①小颖的化简过程从第________步开始出现错误:
②对此整式进行化简。
(1)原式=-2x3y6;(2)①一;②2xy-1 【解析】试题分析: (1)先计算乘方,再计算除法,最后计算乘法即可得; (2)①注意去括号的法则;②根据单项式乘以多项式、完全平方公式以及去括号的法则进行计算即可. 试题解析: (1)原式=-x·4x2y6=-2x3y6 (2)①一; ②【解析】 原式= x2+2xy-(x2+2x+1)+2x =x2+...查看答案和解析>>
科目:初中数学 来源:山东省无棣县2017-2018学年八年级上学期期中考试数学试卷. 题型:单选题
如图,在△ABC中,∠C=90°,∠B=30°,AD是△ABC的角平分线,DE⊥AB,垂足为E,DE=1,则BC=( )
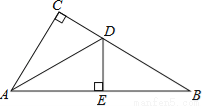
A. 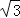 B. 2 C. 3 D.
B. 2 C. 3 D. 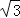 +2
+2
查看答案和解析>>
科目:初中数学 来源:山东省无棣县2017-2018学年八年级上学期期中考试数学试卷. 题型:单选题
剪纸是我国最古老的民间艺术之一,被列入第四批《人类非物质文化遗产代表作名录》,下列剪纸作品中,是轴对称图形的为( )
A.  B.
B.  C.
C.  D.
D. 
查看答案和解析>>
科目:初中数学 来源:北京四中2017-2018学年上学期初中八年级期中考试数学试卷 题型:解答题
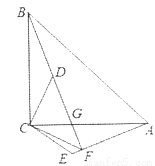
如图,BC⊥CA,BC=CA,DC⊥CE,DC=CE,直线BD与AE交于点F,与AC交于点G,连接CF.
(1)BD和AE的大小关系是____________,位置关系是____________;请给出证明;
(2)求证:CF平分∠BFE.
查看答案和解析>>
科目:初中数学 来源:北京四中2017-2018学年上学期初中八年级期中考试数学试卷 题型:单选题
对于非零实数a、b,规定a?b=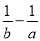 .若2?(2x﹣1)=1,则x的值为( )
.若2?(2x﹣1)=1,则x的值为( )
A. 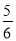 B.
B. 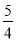 C.
C. 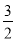 D. ﹣
D. ﹣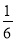
查看答案和解析>>
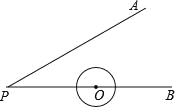
科目:初中数学 来源:天津市宝坻区口东镇2018届九年级12月月考数学试卷 题型:填空题
如图,已知∠APB=30°,OP=3cm,⊙O的半径为1cm,若圆心O沿着BP的方向在直线BP上移动.
(Ⅰ)当圆心O移动的距离为1cm时,则⊙O与直线PA的位置关系是 .
(Ⅱ)若圆心O的移动距离是d,当⊙O与直线PA相交时,则d的取值范围是 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com