
已知:关于x的一元二次方程x2﹣6x﹣m=0有两个实数根.
(1)求m的取值范围;
(2)如果m取符合条件的最小整数,且一元二次方程x2﹣6x﹣m=0与x2+nx+1=0有一个相同的根,求常数n的值.
(1)m≥﹣9;(2 ). 【解析】试题分析:(1)根据判别式的意义得到△=(﹣6)2﹣4×1×(﹣m)≥0,然后解不等式即可得到m的范围; (2)在(1)中m的取值范围内确定满足条件的m的值,再解方程x2﹣6x﹣m=0,然后把它的解代入x2+nx+1=0可计算出n的值. 试题解析:【解析】 (1)根据题意得△=(﹣6)2﹣4×1×(﹣m)≥0,解得m≥﹣9; (2)∵m...科目:初中数学 来源:2016-2017学年黑龙江省哈尔滨市松北区2017届九年级上学期期末数学试卷 题型:填空题
不等式组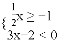 的解集为________.
的解集为________.
查看答案和解析>>
科目:初中数学 来源:2017-2018学年第一学期期末复习备考之精准复习模拟题九年级人教版数学试卷(C卷) 题型:解答题
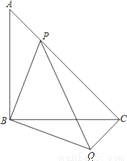
如图,等腰直角△ABC中,∠ABC=90°,点P在AC上,将△ABP绕顶点B沿顺时针方向旋转90°后得到△CBQ.
(1)求∠PCQ的度数;
(2)当AB=4,AP:BP=1:3时,求PQ的长;
(3)当点P在线段AC上运动时(P不与A、C重合),请写出一个反映PA2、PC2、PB2之间关系的等式,并加以证明.
查看答案和解析>>
科目:初中数学 来源:2017-2018学年第一学期期末复习备考之精准复习模拟题九年级人教版数学试卷(C卷) 题型:单选题
如图,一段抛物线:y=﹣x(x﹣2)(0≤x≤2)记为C1,它与x轴交于两点O,A1;将C1绕A1旋转180°得到C2,交x轴于A2;将C2绕A2旋转180°得到C3,交x轴于A3;…如此进行下去,得到Cn,若点P(2017,m)在抛物线Cn上,则m为( )
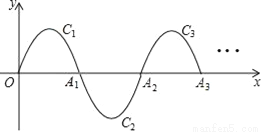
A. 1 B. ﹣1 C. 2 D. ﹣2
A 【解析】∵一段抛物线:y=-x(x-2)(0≤x≤2), ∴图象与x轴交点坐标为:(0,0),(2,0), ∵将C1绕点A1旋转180°得C2,交x轴于点A2; 将C2绕点A2旋转180°得C3,交x轴于点A3; … 如此进行下去,直至得Cn. ∵2017÷2=1008……1, ∴点P(2017,m)在C1009上, ∴C1009的与x轴的...查看答案和解析>>
科目:初中数学 来源:2017-2018学年第一学期期末复习备考之精准复习模拟题九年级人教版数学试卷(C卷) 题型:单选题
设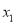 、
、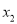 是一元二次方程
是一元二次方程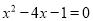 的两个根,则
的两个根,则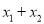 的值为( ).
的值为( ).
A. 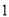 B.
B. 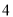 C.
C. 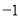 D.
D. 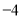
查看答案和解析>>
科目:初中数学 来源:2017-2018学年第一学期期末复习备考之精准复习模拟题九年级人教版数学试卷(A卷) 题型:填空题
已知点A(1,y1),B(-2,y2),C(3,y3)在函数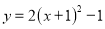 的图像上,试确定y1、y2、y3的大小关系(用“<”表示):__________.
的图像上,试确定y1、y2、y3的大小关系(用“<”表示):__________.
查看答案和解析>>
科目:初中数学 来源:2017-2018学年第一学期期末复习备考之精准复习模拟题九年级人教版数学试卷(A卷) 题型:填空题
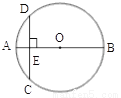
如图,AB是⊙O的直径,CD为⊙O的一条弦,且CD⊥AB于点E,已知CD=4,AE=1,则⊙O的半径为_________.
查看答案和解析>>
科目:初中数学 来源:河南省2017-2018学年八年级(上)第一次月考数学试卷 题型:解答题
如图,△ABC中,AD⊥BC于D,若BD=AD,FD=CD.猜想:BF与AC的关系,并证明.

查看答案和解析>>
科目:初中数学 来源:广西南宁市2017年中考数学一模试卷 题型:单选题
我国是个缺水国家,目前可利用淡水资源总量仅约为899 000乙亿米3 , 其中数据899 000用科学记数法表示为( )
A. 8.99×104 B. 0.899×106 C. 899×103 D. 8.99×105
D 【解析】试题解析:科学记数法的表示形式为a×10n的形式,其中1≤|a|<10,n为整数.确定n的值时,要看把原数变成a时,小数点移动了多少位,n的绝对值与小数点移动的位数相同.当原数绝对值>1时,n是正数;当原数的绝对值<1时,n是负数. 将899 000万用科学记数法表示为8.99×105. 故选D.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com