
如图,小正方形的边长均为1,则下列图形中的三角形与△ABC相似的是( )
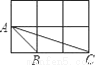
A.  B.
B.  C.
C. 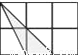 D.
D. 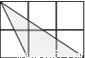
 导学全程练创优训练系列答案
导学全程练创优训练系列答案科目:初中数学 来源:江苏省徐州市区联校2017-2018学年八年级上学期期中联考数学试卷 题型:解答题
如图,△ABC中,AB=AC,AB的垂直平分线交AB于点N,交AC于点M.连 接MB,若AB=8 cm,△MBC的周长是14 cm.
(1)求BC的长;
(2)在直线MN上是否存在点P,使PB+CP的值最小?若存在,直接写出PB+CP的最小值;若不存在,说明理由.

查看答案和解析>>
科目:初中数学 来源:湖南省新化县2016-2017学年度第二学期期中检测七年级数学试卷 题型:单选题
一次课堂练习,王莉同学做了如下4道分解因式题,你认为王莉做得不够完整的一题是( )
A. x3-x=x(x2-1) B. x2-2xy+y2=(x-y)2
C. x2y-xy2=xy(x-y) D. x2-y2=(x-y)(x+y)
A 【解析】A. 提公因式法后还可以运用平方差公式继续分解,应为:原式=x(x+1)(x?1),错误; B. 是完全平方公式,已经彻底,正确; C. 是提公因式法,已经彻底,正确; D. 是平方差公式,已经彻底,正确。 故选A.查看答案和解析>>
科目:初中数学 来源:江苏省扬州市宝应县2018届九年级上学期12月月考数学试卷 题型:填空题
某校要从四名学生中选拔一名参加“汉字听写”大赛,选择赛中每名学生的平均学生的平均成绩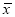 及其方差
及其方差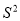 如表所示,如果要选一名成绩高且发挥稳定的学生参赛,则应选择的学生是___.
如表所示,如果要选一名成绩高且发挥稳定的学生参赛,则应选择的学生是___.
甲 | 乙 | 丙 | 丁 | |
| 8 | 9 | 9 | 8 |
| 1 | 1 | 1.2 | 1.3 |
查看答案和解析>>
科目:初中数学 来源:江苏省扬州市宝应县2018届九年级上学期12月月考数学试卷 题型:填空题
当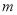 =_____时,关于
=_____时,关于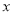 的方程
的方程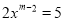 是一元二次方程.
是一元二次方程.
查看答案和解析>>
科目:初中数学 来源:江苏省泰州市2017年中考数学二模试卷(解析版) 题型:解答题
如图,△ABC内接于⊙O,BD为⊙O的直径,BD与AC相交于点H,AC的延长线与过点B的直线相交于点E,且∠A=∠EBC.
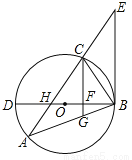
(1)求证:BE是⊙O的切线;
(2)已知CG∥EB,且CG与BD、BA分别相交于点F、G,若BG•BA=48,FG=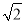 ,DF=2BF,求AH的值.
,DF=2BF,求AH的值.
查看答案和解析>>
科目:初中数学 来源:江苏省泰州市2017年中考数学二模试卷(解析版) 题型:解答题
解不等式组 并写出它的非负整数解.
并写出它的非负整数解.
查看答案和解析>>
科目:初中数学 来源:2017年河南省中考数学三模试卷 题型:解答题
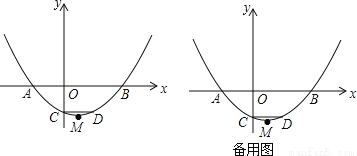
如图,已知抛物线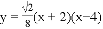 与x轴交于点A、B(点A位于点B左侧),与y轴交于点C,CD∥x轴交抛物线于点D,M为抛物线的顶点.
与x轴交于点A、B(点A位于点B左侧),与y轴交于点C,CD∥x轴交抛物线于点D,M为抛物线的顶点.
(1)求点A、B、C的坐标;
(2)设动点N(-2,n),求使MN+BN的值最小时n的值;
(3)P是抛物线上位于x轴上方的一点,请探究:是否存在点P,使以P、A、B为顶点的三角形与△ABD相似?若存在,求出点P的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源:浙江杭州西湖区保俶塔实验学校2018届九年级上学期期中考试数学试卷(含解析) 题型:填空题
二次函数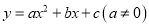 的部分图象如图,图象过点
的部分图象如图,图象过点 ,对称轴为直线
,对称轴为直线 ,下列结论:①
,下列结论:① ;②
;② ;③
;③ ;④当
;④当 时,
时,  的值随
的值随 值的增大而增大;⑤当函数值
值的增大而增大;⑤当函数值 时,自变量
时,自变量 的取值范围是
的取值范围是 或
或 .其中正确的结论有__________.
.其中正确的结论有__________.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com