
 每课必练系列答案
每课必练系列答案 巧学巧练系列答案
巧学巧练系列答案科目:初中数学 来源:2017年天津二十一中中考数学冲刺试卷(一) 题型:单选题
下列说法正确的是( )
A. 一个数的绝对值一定比0大 B. 一个数的相反数一定比它本身小
C. 绝对值等于它本身的数一定是正数 D. 最小的正整数是1
D 【解析】试题分析:分别利用绝对值以及有理数和相反数的定义分析得出即可.A、一个数的绝对值一定比0大,有可能等于0,故此选项错误;B、一个数的相反数一定比它本身小,负数的相反数,比它本身大,故此选项错误;C、绝对值等于它本身的数一定是正数,0的绝对值也等于其本身,故此选项错误;D、最小的正整数是1,正确查看答案和解析>>
科目:初中数学 来源:湖南省新化县2016-2017学年度第二学期期中检测七年级数学试卷 题型:单选题
图①是一个长为2a,宽为2b(a>b)的长方形,用剪刀沿图中虚线(对称轴)剪开,把它分成四块形状和大小都一样的小长方形,然后按图②那样拼成一个正方形,则中间空的部分的面积是( )
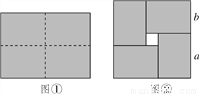
A. ab B. (a+b)2
C. (a-b)2 D. a2-b2
C 【解析】【解析】 中间部分的四边形是正方形,边长是a+b﹣2b=a﹣b,则面积是(a﹣b)2.故选C.查看答案和解析>>
科目:初中数学 来源:江苏省扬州市宝应县2018届九年级上学期12月月考数学试卷 题型:解答题
如图,梯形ABCD中,AD∥BC,对角线AC、BD交于点O,BE∥CD交CA延长线于E 求证:
(1)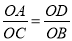 ;(2)
;(2)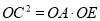
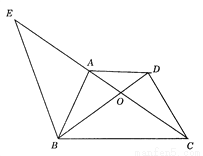
查看答案和解析>>
科目:初中数学 来源:江苏省扬州市宝应县2018届九年级上学期12月月考数学试卷 题型:填空题
如图,在以O为圆心的两个同心圆中,大圆的弦AB与小圆相切于点C,若大圆的半径为5 cm,小圆的半径为3 cm,则弦AB的长为_______cm.

查看答案和解析>>
科目:初中数学 来源:江苏省扬州市宝应县2018届九年级上学期12月月考数学试卷 题型:单选题
如图,小正方形的边长均为1,则下列图形中的三角形与△ABC相似的是( )
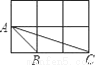
A.  B.
B.  C.
C. 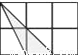 D.
D. 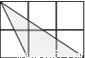
查看答案和解析>>
科目:初中数学 来源:江苏省泰州市2017年中考数学二模试卷(解析版) 题型:解答题
一幢房屋的侧面外墙壁的形状如图所示,它由等腰三角形OCD和矩形ABCD组成,∠OCD=25°,外墙壁上用涂料涂成颜色相同的条纹,其中一块的形状是四边形EFGH,测得FG∥EH,GH=2.6m,∠FGB=65°.
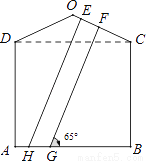
(1)求证:GF⊥OC;
(2)求EF的长(结果精确到0.1m).
(参考数据:sin25°=cos65°≈0.42,cos25°=sin65°≈0.91)
(1)见解析;(2)2.4m. 【解析】试题分析:(1)根据 四边形是矩形, 得出,即可得出答案. (2)根据矩形的判定得出,再利用解直角三角形的知识得出的长. 试题解析:(1)证明:CD与FG交于点M, ∵,四边形ABCD是矩形, ∴ ∴GF⊥CO; (2)作GN⊥EH于点N, ∴四边形ENGF是矩形;查看答案和解析>>
科目:初中数学 来源:江苏省泰州市2017年中考数学二模试卷(解析版) 题型:单选题
如图,在平面直角坐标系xOy中,△A′B′C′由△ABC绕点P旋转得到,则点P的坐标为( )
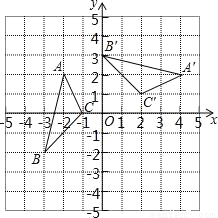
A.(0,1) B.(1,-1) C.(0,-1) D.(1,0)
B. 【解析】 试题解析:由图形可知,对应点的连线CC′、AA′的垂直平分线的交点是点(1,-1),根据旋转变换的性质,点(1,-1)即为旋转中心. 故旋转中心坐标是P(1,-1). 故选B.查看答案和解析>>
科目:初中数学 来源:浙江杭州西湖区保俶塔实验学校2018届九年级上学期期中考试数学试卷(含解析) 题型:解答题
甲、乙、丙三人之间相互传球,球从一个人手中随机传到另一个人手中,
( )若开始时球在甲手中,求经过三次传球后,球传回到甲手中的概率是多少?(用列表法或树状图法说明)
)若开始时球在甲手中,求经过三次传球后,球传回到甲手中的概率是多少?(用列表法或树状图法说明)
( )若乙想使球经过三次传递后,球落在自己手中的概率最大,乙会让球开始时在谁手中?
)若乙想使球经过三次传递后,球落在自己手中的概率最大,乙会让球开始时在谁手中?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com