
��ͼ������������y����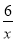 �ڵڶ�����ͼ����������A��B�����ǵĺ�����ֱ�Ϊ��1����3��ֱ��AB��x�ύ�ڵ�C�����AOC�����Ϊ( )
�ڵڶ�����ͼ����������A��B�����ǵĺ�����ֱ�Ϊ��1����3��ֱ��AB��x�ύ�ڵ�C�����AOC�����Ϊ( )

A. 8 B. 10 C. 12 D. 24
C �����������������x=-1ʱ��y=6��x=-3ʱ��y=2�����Ե�A��-1��6������B��-3��2����Ӧ�ô���ϵ�������ֱ��AB�Ľ���ʽΪy=2x+8��ֱ��AB��x��Ľ���C��-4��0��������OC=4����A ��x��ľ���Ϊ6�����ԡ�AOC�����Ϊ=12�� ��ѡ��C�� �ظ���ʦ�㲦ϵ�д�
�ظ���ʦ�㲦ϵ�д� �ľ�ͼ���ʱ�ȷ�ϵ�д�
�ľ�ͼ���ʱ�ȷ�ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ��2017-2018ѧ����꼶��ѧ��ʦ����ϲ� ȫ���ۺϲ��Ծ�1 ���ͣ������
��̽��֤����
(1)ij����ѧ����ѧϰС��Ծ������������ഹֱ���߶���������ڱߵ�������ϵ����̽��������������⣬�������֤����
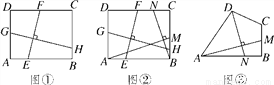
��ͼ�٣��ھ���ABCD�У�EF��GH��EF�ֱ�AB��CD�ڵ�E��F��GH�ֱ�AD��BC�ڵ�G��H.��֤�� 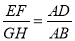 ��
��
������Ӧ�á�
(2)��ͼ�ڣ�������(1)�������£���AM��BN����M��N�ֱ��ڱ�BC��CD�ϣ���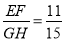 ����
����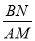 ��ֵΪ ��
��ֵΪ ��
����ϵ��չ��
(3)��ͼ�ۣ��ı���ABCD�У���ABC=90�㣬AB=AD=10��BC=CD=5��AM��DN����M��N�ֱ��ڱ�BC��AB�ϣ���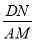 ��ֵ��
��ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ������ʡ�żҸ���2017-2018ѧ���һѧ�ڳ�����ѧ��ĩ�����Ծ� ���ͣ������
������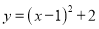 ����Сֵ��_________.
����Сֵ��_________.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2018�˽̰���꼶��ѧ�²���ϰ�����м��� ���ͣ������
��ͼ����֪����������y��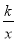 ��ͼ����A(��1��
��ͼ����A(��1�� 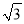 )��
)��
(1)��ȷ���˷����������Ľ���ʽ��
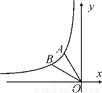
(2)��O������ԭ�㣬���߶�OA�Ƶ�O��ʱ����ת30���õ��߶�OB�������B�����꣬���жϵ�B�Ƿ��ڴ˷�����������ͼ���ϣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2018�˽̰���꼶��ѧ�²���ϰ�����м��� ���ͣ������
��ͼ���ڡ�ABC�У�D��E�ֱ��DZ�AB��AC�ϵĵ㣬��DE��BC������ADE���ABC���ܳ�֮��Ϊ2��3��AD��4����DB��_______��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2018�˽̰���꼶��ѧ�²���ϰ�����м��� ���ͣ���ѡ��
��A(��1��y1)��B(��2��y2)�ڷ���������y��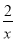 ��ͼ���ϣ���y1��y2�Ĵ�С��ϵ�ǣ� ��
��ͼ���ϣ���y1��y2�Ĵ�С��ϵ�ǣ� ��
A. y1��y2 B. y1��y2 C. y1��y2 D. ����ȷ��
C ���������ȸ��ݷ����������Ľ���ʽ�жϳ�������������ͼ�����ڵ������������ԣ��ٸ���A��B����ĺ������жϳ��������ڵ����ޣ��������ó�����. �������� �߷���������y=�У�k=2>0�� ��˺���ͼ���������֧�ֱ�λ��һ�������ޣ�����ÿһ������y��x���������С, �ߣ�-1<0��-2<0�� ���A��-1��y1����B��-2��y2����λ�ڵ������ޣ� ��-1>--2...�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ����ʦ������꼶�²���ѧ �ڶ��� �ཻ����ƽ���� ��Ԫ���� ���ͣ������
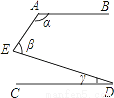
��֪����ͼ��AB��CD����Ϧ����Ϧ¡��Ϧ�֮��Ĺ�ϵΪ________
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ����ʦ������꼶��ѧ�²����� ������ ����֮��Ĺ�ϵ ���ͣ������
��ͼ,һ���뾶Ϊ18 cm��Բ,��������ȥһ��������,����ȥ�������εı߳���С���ʱ,ʣ�²��ֵ����Ҳ��֮�����仯.
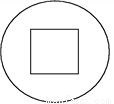
(1)����ȥ�������α߳�Ϊx(cm),ʣ�²��ֵ����Ϊy(cm2),��y��x֮��Ĺ�ϵʽ��ʲô?
(2)����ȥ�������εı߳���1 cm�仯��9 cmʱ,ʣ�²��ֵ������____�仯��____.
(324��-1)cm2 (324��-81)cm2 ��������������(1)ʣ�²��ֵ����y���Ǵ�Բ���������ȥ�������ε�����IJ (2)�ں�������ʽ�зֱ�����뾶x���ֱ���1cm��9cmʱ�������ֵ���������. ��������� ��1��y��x֮��Ĺ�ϵʽΪ��y= �� ��2������ȥԲ�İ뾶Ϊ1cmʱ���ɣ�1��������ĺ�����ϵʽ�ɵã�Բ�����:y=324��-1²=(323��-1)...�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ����ʦ������꼶��ѧ�²�4.2ͼ�ε�ȫ����ϰ ���ͣ������
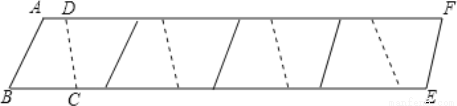
��ͼ��ʾ��ͼ������ȫ�ȵ�ͼ��ƴ�ɵģ�����AD=0.5cm��BC=1cm����AF�ij���Ϊ���٣�
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com