练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

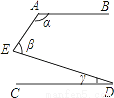
    已知，如图，AB∥CD，则∠α、∠β、∠γ之间的关系为________

    ∠α+∠β﹣∠γ=180° 【解析】利用平行线的性质及判定即可得出答案. 【解析】 如图所示，过点E引一条直线EF∥AB， ∵EF∥AB， ∴∠α+∠AEF=180°． ∵AB∥CD，EF∥AB， ∴EF∥CD， ∴∠FED =∠γ， ∴∠α+∠AEF+∠FED =180°+∠γ， ∴∠α+∠β=180°+∠γ， 即∠α+∠β－∠γ=1...
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源：2017-2018学年九年级数学北师大版上册 全册综合测试卷1 题型：填空题

    从甲、乙2名医生和丙、丁2名护士中任意抽取2人参加医疗队，那么抽取的2人恰好是一名医生和一名护士的概率为________．

    【解析】【解析】 画树状图为： 共有12种等可能的结果数，其中恰好是一名医生和一名护士的结果数为8，所以恰好是一名医生和一名护士的概率==．故答案为： ．

    查看答案和解析>>

    科目：初中数学 来源：2018人教版九年级数学下册练习：期中检测卷 题型：解答题

    如图，在平面直角坐标系xOy中，直线y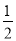＝x＋2与x轴交于点A，与y轴交于点C.抛物线y＝ax2＋bx＋c的对称轴是直线x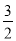＝－，且经过A，C两点，与x轴的另一交点为点B.

    (1)①直接写出点B的坐标；②求抛物线的解析式．

    (2)抛物线上是否存在点M，过点M作MN垂直x轴于点N，使得以点A，M，N为顶点的三角形与△ABC相似？若存在，求出点M的坐标；若不存在，请说明理由．

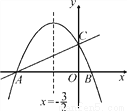
    (1)①点B的坐标为(1，0)；②y＝－x2－x＋2；(2)存在点M1(0，2)，M2(－3，2)，M3(2，－3)，M4(5，－18)，使得以点A，M，N为顶点的三角形与△ABC相似. 【解析】【试题分析】（1）①先求的直线y=x+2与x轴、y轴交点的坐标，然后利用抛物线的对称性可求得点B的坐标；②设抛物线的解析式为y=y=a（x+4）（x﹣1），然后将点C的坐标代入即可求得a的值；（3）...

    查看答案和解析>>

    科目：初中数学 来源：2018人教版九年级数学下册练习：期中检测卷 题型：单选题

    如图，反比例函数y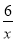＝－在第二象限的图象上有两点A，B，它们的横坐标分别为－1，－3，直线AB与x轴交于点C，则△AOC的面积为( )

    A. 8 B. 10 C. 12 D. 24

    C 【解析】试题分析：x=-1时，y=6，x=-3时，y=2，所以点A（-1，6），点B（-3，2），应用待定系数法求得直线AB的解析式为y=2x+8，直线AB与x轴的交点C（-4，0），所以OC=4，点A 到x轴的距离为6，所以△AOC的面积为=12． 故选：C．

    查看答案和解析>>

    科目：初中数学 来源：2018人教版九年级数学下册练习：期中检测卷 题型：单选题

    下列各点中，在函数y=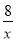－图象上的是（ ）

    A．（﹣2，4） B．（2，4） C．（﹣2，﹣4） D．（8，1）

    A 【解析】 试题分析：所有在反比例函数上的点的横纵坐标的积应等于比例系数．本题只需把所给点的横纵坐标相乘，结果是﹣8的，就在此函数图象上

    查看答案和解析>>

    科目：初中数学 来源：北师大版七年级下册数学 第二章 相交线与平行线 单元检测卷 题型：填空题

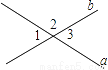
    如图，直线a、b相交，∠1=36度，则∠2=________度．

    144 【解析】根据邻补角的定义即可解答. 【解析】 ∵直线a、b相交， ∴∠1+∠2=180°， ∵∠1=36°， ∴∠2=180°－36°=144°. 故答案为：144.

    查看答案和解析>>

    科目：初中数学 来源：北师大版七年级下册数学 第二章 相交线与平行线 单元检测卷 题型：单选题

    如图所示，在三角形ABC中，点D是边AB上的一点．已知∠ACB=90°，∠CDB=90°，则图中与∠A互余的角的个数是（　　）

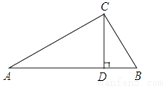
    A. 1 B. 2 C. 3 D. 4

    B 【解析】根据图形和余角的概念即可解答. 【解析】 ∵∠ACB=90°， ∴∠A+∠B=90°， ∵∠CDB=90°， ∴∠A+∠ACD=90°， ∴与∠A互余的角有两个. 故选B.

    查看答案和解析>>

    科目：初中数学 来源：北师大版七年级数学下册达标检测 第三章 变量之间的关系 题型：单选题

    某校组织学生到距学校6 km的光明科技馆参观.王红准备乘出租车去科技馆,出租车的收费标准如下表:

    里程数

    收费/元

    3 km以下(含3 km)

    8.00

    3 km以上每增加1 km

    1.80

    则收费y(元)与出租车行驶里程数x(km)(x≥3)之间的关系式为(　　)

    A. y=8x B. y=1.8x C. y=8+1.8x D. y=2.6+1.8x

    D 【解析】∵3千米以上每增加1千米收费1.80元， ∴出租车行驶里程数x(x≥3)与收费y之间的关系式为： y=8+1.8(x-3)=1.8x+2.6. 故选：D.

    查看答案和解析>>

    科目：初中数学 来源：2018人教版七年级数学下册练习：第五章达标检测卷 题型：解答题

    (1)在图①中以P为顶点画∠P,使∠P的两边分别和∠1的两边垂直;

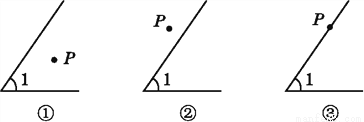
    (2)量一量∠P和∠1的度数,它们之间的数量关系是　　　　　　　　; 

    (3)同样在图②和图③中以P为顶点作∠APB,使∠APB的两边分别和∠1的两边垂直,分别写出图②和图③中∠APB和∠1之间的数量关系(不要求写出理由).

    图②:　　　　　　　　　　　　　　　　, 

    图③:　　　　　　　　　　　　　　　　; 

    (4)由上述三种情形可以得到一个结论:如果一个角的两边分别和另一个角的两边垂直,那么这两个角　　　　(不要求写出理由).

    （1）作图见解析；（2）∠1+∠P=180°；（3）.∠1=∠APB;∠1=∠APB或∠1+∠APB=180°(4)相等或互补 【解析】试题分析：（1）根据题目要求，结合题中条件，由点P分别向∠1的两边做垂线，即可得到∠P； （2）用量角器分别测量∠P与∠1的度数，即可得出二者的关系； （3）分别在其余两图中，按要求作出∠P，再测量，即可得到结论； （4）结合以上作图和结论...

    查看答案和解析>>

    同步练习册答案