
已知:⊙O的半径为25cm,弦AB=40cm,弦CD=48cm,AB∥CD.求这两条平行弦AB,CD之间的距离______________.
8cm或22cm 【解析】(1)如图1,连接OB,OD,做OM⊥AB交CD于点N, ∵AB∥CD, ∴ON⊥CD, ∵AB=40cm,CD=48cm, ∴BM=20cm,DN=24cm, ∵⊙O的半径为25cm, ∴OB=OD=25cm, ∴OM=15cm,ON=7cm, ∵MN=OM-ON, ∴MN=8cm, (2)如图2,连接OB,OD,做直线OM⊥AB交CD于点... 暑假衔接教材期末暑假预习武汉出版社系列答案
暑假衔接教材期末暑假预习武汉出版社系列答案 假期作业暑假成长乐园新疆青少年出版社系列答案
假期作业暑假成长乐园新疆青少年出版社系列答案科目:初中数学 来源:山东省潍坊市诸城市2016-2017学年八年级(上)期末数学试卷 题型:单选题
一艘海轮位于灯塔P的南偏东70°方向的M处,它以每小时40海里的速度向正北方向航行,2小时候到达位于灯塔P的北偏东40°的N处,则N处与灯塔P的距离为( )
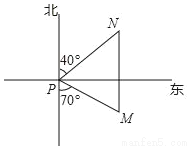
A. 80海里 B. 70海里 C. 60海里 D. 40海里
A 【解析】【解析】 如图,∵MN∥PF,∠1=40°,∠2=70°,由三角形的内角和,得 ∠3=180°﹣∠1﹣∠2=180°﹣40°﹣70°=70°. ∵∠3=∠2=70°,∴PN=MN=2×40=80海里,故选A.查看答案和解析>>
科目:初中数学 来源:吉林省2017-2018学年度七年级数学上册期末测试卷 题型:填空题
已知y1=x+3,y2=2-x,当x=_________时,y1比y2大5.
2 【解析】根据题意得:(x+3)-(2-x)=5, 去括号得:x+3-2+x=5, 移项合并得:2x=4, 解得:x=2, 则当x=2时,y1比y2大5, 故答案为:2查看答案和解析>>
科目:初中数学 来源:吉林省2017-2018学年度七年级数学上册期末测试卷 题型:单选题
在墙壁上固定一根横放的木条,则至少需要钉子的枚数是( )
A. 1枚 B. 2枚 C. 3枚 D. 任意枚
B 【解析】【解析】 ∵两点确定一条直线, ∴至少需要2枚钉子. 故选B.查看答案和解析>>
科目:初中数学 来源:2017-2018学年内蒙古乌兰察布市分校九年级(上)期中数学试卷 题型:解答题
已知抛物线的顶点为(1,﹣4),且过点(﹣2,5).
(1)求抛物线解析式;
(2)直接写出当函数值y>0时,自变量x的取值范围.
(1)y=(x﹣1)2﹣4;(2)x<﹣1或x>3. 【解析】试题分析: (1)由已知可设抛物线解析式为: ,代入点(-2,5)即可解得的值,从而可求得抛物线的解析式; (2)在(1)中所得抛物线的解析式中,由可得一元二次方程,解方程即可求得对应的的值,结合抛物线的开口方向,即可求得时,自变量的取值范围. 试题解析: (1)由已知可设抛物线解析式为: , 把点(...查看答案和解析>>
科目:初中数学 来源:2017-2018学年内蒙古乌兰察布市分校九年级(上)期中数学试卷 题型:单选题
如图,点C是以点O为圆心,AB为直径的半圆上的动点(点C不与点A,B重合),AB=4.设弦AC的长为x,△ABC的面积为y,则下列图象中,能表示y与x的函数关系的图象大致是( )
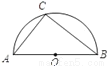
A. 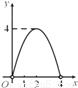 B.
B. 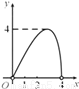 C.
C. 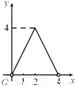 D.
D. 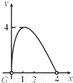
查看答案和解析>>
科目:初中数学 来源:2017-2018学年内蒙古乌兰察布市分校九年级(上)期中数学试卷 题型:单选题
若(2,5)、(4,5)是抛物线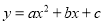 上的两个点则它的对称轴( )
上的两个点则它的对称轴( )
A. x=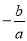 B.
B. 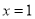 C.
C. 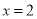 D.
D. 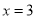
查看答案和解析>>
科目:初中数学 来源:甘肃省白银市2018届九年级(上)期中数学试卷 题型:填空题
如图是某地的灌溉系统,一个漂浮物A流到B处的概率为______.
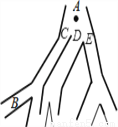
查看答案和解析>>
科目:初中数学 来源:广东省深圳市龙岗区2018届九年级上学期期中考试数学试卷 题型:解答题
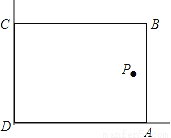
在美化校园的活动中,某综合实践小组的同学借如图所示的直角墙角(两边足够长),用28m长的篱笆围成一个矩形的花圃ABCD(篱笆只围AB、BC两边)设AB=xm.
(1)若想围得花圃面积为192cm2,求x的值;
(2)若在点P处有一棵小树与墙CD、AD的距离分别为15m和6m,要将这棵树围在花圃内(含边界,不考虑树干的粗细),求花圃面积S的最大值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com