
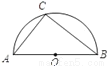
如图,点C是以点O为圆心,AB为直径的半圆上的动点(点C不与点A,B重合),AB=4.设弦AC的长为x,△ABC的面积为y,则下列图象中,能表示y与x的函数关系的图象大致是( )
A. 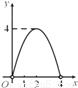 B.
B. 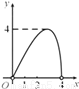 C.
C. 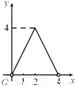 D.
D. 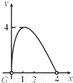
科目:初中数学 来源:山东省潍坊市诸城市2016-2017学年八年级(上)期末数学试卷 题型:单选题
若3x﹣2y=0,则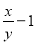 等于( )
等于( )
A. 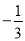 B.
B. 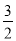 C.
C. 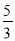 D.
D. 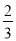
查看答案和解析>>
科目:初中数学 来源:吉林省2017-2018学年度七年级数学上册期末测试卷 题型:填空题
单项式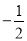 xy2的系数是_________.
xy2的系数是_________.
查看答案和解析>>
科目:初中数学 来源:2017-2018学年内蒙古乌兰察布市分校九年级(上)期中数学试卷 题型:解答题
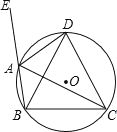
如图,四边形ABCD内接于⊙O,∠DAE是四边形ABCD的一个外角,且AD平分∠CAE.
求证:DB=DC.
查看答案和解析>>
科目:初中数学 来源:2017-2018学年内蒙古乌兰察布市分校九年级(上)期中数学试卷 题型:解答题
已知:⊙O的半径为25cm,弦AB=40cm,弦CD=48cm,AB∥CD.求这两条平行弦AB,CD之间的距离______________.
8cm或22cm 【解析】(1)如图1,连接OB,OD,做OM⊥AB交CD于点N, ∵AB∥CD, ∴ON⊥CD, ∵AB=40cm,CD=48cm, ∴BM=20cm,DN=24cm, ∵⊙O的半径为25cm, ∴OB=OD=25cm, ∴OM=15cm,ON=7cm, ∵MN=OM-ON, ∴MN=8cm, (2)如图2,连接OB,OD,做直线OM⊥AB交CD于点...查看答案和解析>>
科目:初中数学 来源:2017-2018学年内蒙古乌兰察布市分校九年级(上)期中数学试卷 题型:单选题
在同一平面直角坐标系内,一次函数y=ax+b与二次函数y=ax2+5x+b的图象可能是( )
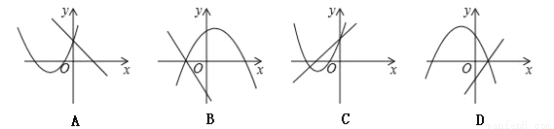
查看答案和解析>>
科目:初中数学 来源:甘肃省白银市2018届九年级(上)期中数学试卷 题型:解答题
已知:平行四边形ABCD的两边AB、AD的长是关于x的方程x2﹣mx+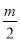 -
-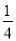 =0的两个实数根.
=0的两个实数根.
(1)m为何值时,四边形ABCD是菱形?求出这时菱形的边长;
(2)若AB的长为2,那么平行四边形ABCD的周长是多少?
(1)m=1时,四边形ABCD是菱形,菱形ABCD的边长是;(2)平行四边形ABCD的周长是5. 【解析】试题分析: (1)∵四边形ABCD是菱形, ∴AB=AD, ∴△=0,即m2﹣4(﹣)=0, 整理得:(m﹣1)2=0, 解得m=1, 当m=1时,原方程为x2﹣x+=0, 解得:x1=x2=0.5, 故当m=1时,四边形ABCD是菱形,菱形的边...查看答案和解析>>
科目:初中数学 来源:甘肃省白银市2018届九年级(上)期中数学试卷 题型:单选题
如图,在正方形ABCD的外侧,作等边三角形ADE,AC、BE相交于点F,则∠BFC为( )
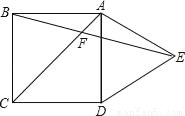
A. 45° B. 55° C. 60° D. 75°
C 【解析】∵四边形ABCD是正方形, ∴AB=AD, 又∵△ADE是等边三角形, ∴AE=AD=DE,∠DAE=60°, ∴AB=AE, ∴∠ABE=∠AEB,∠BAE=90°+60°=150°, ∴∠ABE=(180°?150°)÷2=15°, 又∵∠BAC=45°, ∴∠BFC=45°+15°=60°. 故选:C.查看答案和解析>>
科目:初中数学 来源:广东省深圳市龙岗区2018届九年级上学期期中考试数学试卷 题型:填空题
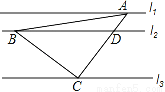
如图,直线l1∥l2∥l3,一等腰直角三角形ABC的三个顶点A、B、C分别在l1、l2、l3上,AC交l2于D,∠ACB=90°.已知l1与l2的距离为2,l2与l3的距离为6,则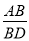 的值为_____.
的值为_____.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com