
如图是甲、乙两车在某时段速度随时间变化的图象,下列结论错误的是( )
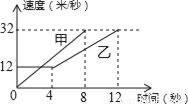
A. 乙前4秒行驶的路程为48米
B. 在0到8秒内甲的速度每秒增加4米/秒
C. 两车到第3秒时行驶的路程相等
D. 在4至8秒内甲的速度都大于乙的速度
【答案】C
【解析】试题分析:A.根据图象可得,乙前4秒行驶的路程为12×4=48米,正确;
B.根据图象得:在0到8秒内甲的速度每秒增加4米秒/,正确;
C.根据图象可得两车到第3秒时行驶的路程不相等,故本选项错误;
D.在4至8秒内甲的速度都大于乙的速度,正确;
故选C.
考点:函数的图象.
【题型】单选题
【结束】
8
若实数a、b、c满足a+b+c=0,且a<b<c,则函数y=ax+c的图象可能是 ( ) .
A. 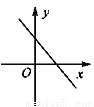 B.
B. 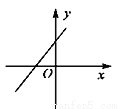 C.
C. 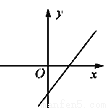 D.
D. 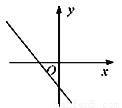
 课课练江苏系列答案
课课练江苏系列答案 名牌中学课时作业系列答案
名牌中学课时作业系列答案 明天教育课时特训系列答案
明天教育课时特训系列答案 浙江新课程三维目标测评课时特训系列答案
浙江新课程三维目标测评课时特训系列答案科目:初中数学 来源:江苏省丹阳市2017-2018学年八年级12月月考数学试卷 题型:解答题
已知y=(k﹣1)x|k|﹣k+2是一次函数,
(1)求k的值;(2)若点(-5,m)在这个一次函数的图象上,求m的值.
(1)k=-1;(2)m=13 【解析】试题分析:(1)由一次函数的定义可知: 且,从而可求得的值; (2)将点的坐标代入函数的解析式,从而可求得的值. 试题解析:(1)∵y是一次函数, ∴|k|=1,解得k=±1. 又∵k?1≠0, ∴k≠1. ∴k=?1. (2)将k=?1代入得一次函数的解析式为y=?2x+3. ∵(-5,m)在y=?2x+3...查看答案和解析>>
科目:初中数学 来源:江苏省2018届九年级12月月考数学试卷 题型:单选题
设A(﹣2,y1),B(1,y2),C(2,y3)是抛物线y=﹣(x+1)2+1上的三点,则y1,y2,y3的大小关系为( )
A. y1>y2>y3 B. y1>y3>y2 C. y3>y2>y1 D. y3>y1>y2
A 【解析】把A(﹣2,y1),B(1,y2),C(2,y3)代入抛物线有, y1=0,y2=-3,y3=-8, y1>y2>y3。 选A.查看答案和解析>>
科目:初中数学 来源:郑州二中学区2017-2018学年上学期期中学业水平测试 八年级数学试卷 题型:解答题
如图,△ACB和△ECD都是等腰直角三角形,∠ACB=∠ECD=90°,D为AB边上一点,求证:
(1)△ACE≌△BCD;(2)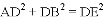 .
.
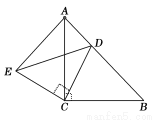
【答案】(1)证明见解析;(2)证明见解析.
【解析】试题分析:(1)本题要判定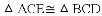
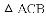
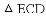
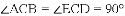
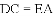
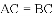

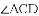

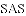
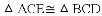
(2)由(1)的论证结果得出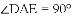
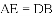
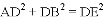 .
.
试题解析:
(1)∵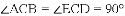
∴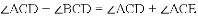
∴
∵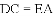
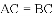
∴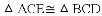
(2)∵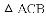
∴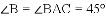
∵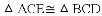
∴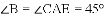
∴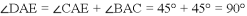
∴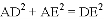 .
.
由(1)知AE=DB,
∴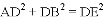 .
.
考点:(1)勾股定理;(2)全等三角形的判定与性质;(3)等腰直角三角形.
【题型】解答题
【结束】
20
已知一次函数y=2x+4
(1)在如图所示的平面直角坐标系中,画出函数的图象;
(2)求图象与x轴的交点A的坐标,与y轴交点B的坐标;
(3)在(2)的条件下,求出△AOB的面积;
(4)利用图象直接写出:当y<0时,x的取值范围.
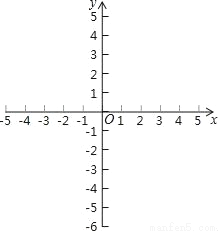
查看答案和解析>>
科目:初中数学 来源:郑州二中学区2017-2018学年上学期期中学业水平测试 八年级数学试卷 题型:填空题
在平面直角坐标系中,已知一次函数y=2x+1的图象经过P1(x1,y1)、P2(x2,y2)两点,若x1<x2,则y1 ______ y2.(填“>”“<”或“=”)
【答案】<
【解析】试题解析:∵一次函数y=2x+1中k=2>0,
∴y随x的增大而增大,
∵x1<x2,
∴y1<y2.
考点:一次函数图象上点的坐标特征.
【题型】填空题
【结束】
13
如图,在矩形ABCD中,AB=3,BC=5,在CD上任取一点E,连接BE,将△BCE沿BE折叠,使点C恰好落在AD边上的点F处,则CE的长为_____.
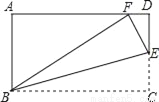
查看答案和解析>>
科目:初中数学 来源:郑州二中学区2017-2018学年上学期期中学业水平测试 八年级数学试卷 题型:单选题
以下列数组作为三角形的三条边长,其中能构成直角三角形的是( )
A. 1, 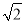 ,3 B.
,3 B. 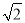 ,
, 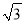 ,5 C. 1.5,2,2.5 D.
,5 C. 1.5,2,2.5 D. 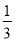 ,
, 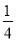 ,
, 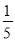
【答案】C
【解析】A、12+(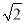 )2≠32,不能构成直角三角形,故选项错误;
)2≠32,不能构成直角三角形,故选项错误;
B、(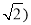 2+(
2+(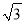 )2≠52,不能构成直角三角形,故选项错误;
)2≠52,不能构成直角三角形,故选项错误;
C、1.52+22=2.52,能构成直角三角形,故选项正确;
D、(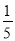 ))2+(
))2+(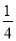 )2≠(
)2≠(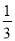 )2,不能构成直角三角形,故选项错误.
)2,不能构成直角三角形,故选项错误.
故选:C.
【题型】单选题
【结束】
3
在Rt△ABC中,∠C=90°,AC=9,BC=12,则点C到斜边AB的距离是( )
(A) (B)
(B) (C)9 (D)6
(C)9 (D)6
查看答案和解析>>
科目:初中数学 来源:人教版九年级数学上册经典试卷 第21章 一元二次方程韦达定理 测试卷 题型:解答题
关于x的方程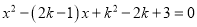 有两个不相等的实数根.
有两个不相等的实数根.
(1)求实数k的取值范围;
(2)设方程的两个实数根分别为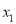 、
、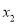 ,存不存在这样的实数k,使得
,存不存在这样的实数k,使得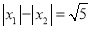 ?若存在,求出这样的k值;若不存在,说明理由.
?若存在,求出这样的k值;若不存在,说明理由.
查看答案和解析>>
科目:初中数学 来源:人教版九年级数学上册经典试卷 第21章 一元二次方程韦达定理 测试卷 题型:单选题
小明和小华解同一个一元二次方程时,小明看错一次项系数,解得两根为2,﹣3,而小华看错常数项,解错两根为﹣2,5,那么原方程为( )
A. x2﹣3x+6=0 B. x2﹣3x﹣6=0 C. x2+3x﹣6=0 D. x2+3x+6=0
B 【解析】试题分析:小明看错一次项系数,解得两根为2,﹣3,两根之积正确;小华看错常数项,解错两根为﹣2,5,两根之和正确,故设这个一元二次方程的两根是α、β,根据一元二次方程根与系数的关系x1+x2=-,x1•x2=,可得:α•β=﹣6,α+β=﹣3,那么以α、β为两根的一元二次方程就是x2﹣3x﹣6=0, 故选:B.查看答案和解析>>
科目:初中数学 来源:天津市 2017-2018学年 九年级数学上册 一元二次方程 因式分解法 专题练习(含答案) 题型:填空题
方程3(x-5)2=2(x-5)的根是__
x1=5,x2= 【解析】试题解析:方程变形得:3(x-5)2-2(x-5)=0, 分解因式得:(x-5)[3(x-5)-2]=0, 可得x-5=0或3x-17=0, 解得:x1=5,x2=.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com