
如图,在△ABC中,∠BAC=90°,AD⊥BC于D,若AB=3,AC=4,则sin∠DAC的值为( )
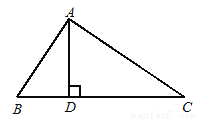
A. 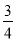 B.
B. 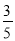 C.
C. 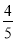 D.
D. 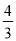
科目:初中数学 来源:安徽省六安市2018届九年级上学期第二次月考数学试卷 题型:单选题
如图,在△ABC,P为AB上一点,连结CP,下列条件中不能判定△ACP∽△ABC的是( )

A. ∠ACP=∠B B. ∠APC=∠ACB C.  D.
D. 
查看答案和解析>>
科目:初中数学 来源:云南省2018届九年级上学期期中考试数学试卷 题型:解答题
已知⊙O的直径为10,点A,点B,点C在⊙O上,∠CAB的平分线交⊙O于点D
(1)如图①,若BC为⊙O的直径,AB=6,求AC,BD,CD的长;
(2)如图②,若∠CAB=60°,求BD的长.
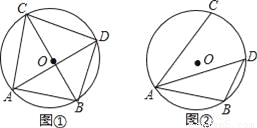
查看答案和解析>>
科目:初中数学 来源:2017-2018学年度第一学期海南省海口市九年级数学科期末检测题 题型:解答题
如图,一艘轮船从离A观察站的正北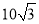 海里处的B港出发向东航行,观察站第一次测得该船在A地北偏东30°的C处;半小时后,又测得该船在A地的北偏东60°的D处,求此船的速度.
海里处的B港出发向东航行,观察站第一次测得该船在A地北偏东30°的C处;半小时后,又测得该船在A地的北偏东60°的D处,求此船的速度.
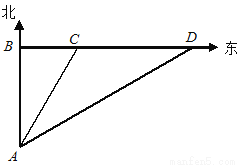
查看答案和解析>>
科目:初中数学 来源:2017-2018学年度第一学期海南省海口市九年级数学科期末检测题 题型:填空题
已知关于x的方程x2-2x+m=0的一个根是x=1-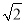 ,则m=___________ .
,则m=___________ .
查看答案和解析>>
科目:初中数学 来源:2017-2018学年度第一学期海南省海口市九年级数学科期末检测题 题型:单选题
从1~10这十个数中随机取出一个数,取出的数是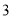 的倍数的概率是( )
的倍数的概率是( )
A. 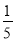 B.
B. 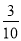 C.
C. 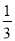 D.
D. 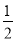
查看答案和解析>>
科目:初中数学 来源:安徽省2017-2018学年度七年级第一学期人教版数学期末自测试卷(二) 题型:解答题
如图所示,OE是∠AOD的平分线,OC是∠BOD的平分线.
(1)若∠AOB=130°,则∠COE是多少度?
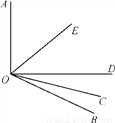
(2)在(1)的条件下,若∠COD=20°,则∠BOE是多少度?
(1) 65°(2) 85° 【解析】试题分析:(1)直接根据角平分线的定义进行解答即可; (2)先根据∠COD=20°求出∠BOD的度数,再根据∠AOB=130°求出∠AOD的度数,根据角平分线的定义即可得出结论. 试题解析:(1)∵OC是∠AOD的平分线,OE是∠BOD的平分线,∠AOB=130° ∴∠COE=∠BOD+∠AOD=(∠BOD+∠AOD)=∠AOB=65°; ...查看答案和解析>>
科目:初中数学 来源:安徽省2017-2018学年度七年级第一学期人教版数学期末自测试卷(二) 题型:单选题
下列运算正确的是( )
A. 5x-3x=2 B. 2a+3b=5ab
C. -(a-b)=b+a D. 2ab-ba=ab
D 【解析】根据合并同类项,去括号的方法计算. A、5x-3x=2x.错误; B、2a与3b不是同类项,不能合并.错误; C、-(a-b)=b-a.错误; D、2ab-ba=ab.正确. 故选D.查看答案和解析>>
科目:初中数学 来源:辽宁省2018届九年级(上)期末模拟数学试卷 题型:填空题
公元3世纪,我国古代数学家刘徽就能利用近似公式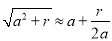 得到的近似值.他的算法是:先将
得到的近似值.他的算法是:先将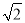 看出
看出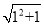 :由近似公式得到
:由近似公式得到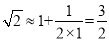 ;再将
;再将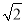 看成
看成  ,由近似值公式得到
,由近似值公式得到 ;…依此算法,所得
;…依此算法,所得 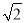 的近似值会越来越精确.当
的近似值会越来越精确.当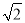 取得近似值
取得近似值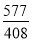 时,近似公式中的a是________,r是________.
时,近似公式中的a是________,r是________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com