
计算:(﹣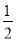 +1)×
+1)×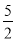 +
+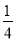 ﹣|(﹣1
﹣|(﹣1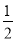 )3|÷
)3|÷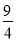 .
.
 期末冲刺100分创新金卷完全试卷系列答案
期末冲刺100分创新金卷完全试卷系列答案科目:初中数学 来源:2017年湖北省中考数学模拟试卷 题型:填空题
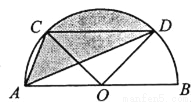
如图,半圆O的直径AB=2,弦CD∥AB,∠COD=90°,则图中阴影部分的面积为_____.
查看答案和解析>>
科目:初中数学 来源:江苏省无锡市2017-2018学年七年级12月月考数学试卷 题型:解答题
定义一种新运算:观察下列各式:
1⊙3=1×4+3=7 ; 3⊙(-1)= 3×4-1=11 ;
5⊙4=5×4+4=24 ; 4⊙(-3)= 4×4-3=13 .
(1)请你想一想:a⊙b=___________;
(2)若a≠b,那么a⊙b______b⊙a(填入 “=”或 “≠ ”) ;
(3)若a⊙(-2b) = 4,请计算 (a-b)⊙(2a+b)的值.
(1)4a+b;(2)≠;(3)6. 【解析】试题分析:(1)根据提供的信息,⊙的运算法则是⊙前面的数乘以4再加上运算符号后面的数,然后写出即可; (2)根据运算规则把a⊙b和b⊙a分别进行计算并相减得到a、b的差,然后即可比较大小; (3)先根据运算规则与已知条件求出a、b的关系,然后再根据运算规则计算(a-b)⊙(2a+b)并把a、b的关系代入整理后的算式计算即可求解. ...查看答案和解析>>
科目:初中数学 来源:江苏省无锡市2017-2018学年七年级12月月考数学试卷 题型:单选题
如图,把左边的图形绕着给定的直线旋转一周后形成的几何体是( )

A. 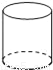 B.
B. 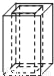 C.
C. 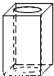 D.
D. 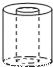
查看答案和解析>>
科目:初中数学 来源:2017年河北省中考数学模拟试卷 题型:解答题
如图,水库大坝的横断面为四边形ABCD,其中AD∥BC,坝顶BC=10米,坝高20米,斜坡AB的坡度i=1:2.5,斜坡CD的坡角为30°.
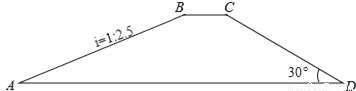
(1)求坝底AD的长度(结果精确到1米);
(2)若坝长100米,求建筑这个大坝需要的土石料(参考数据: 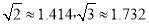 )
)
查看答案和解析>>
科目:初中数学 来源:2017年河北省中考数学模拟试卷 题型:单选题
如图,点A的坐标为(0,1),点B是x轴正半轴上的一动点,以AB为边作等腰Rt△ABC,使∠BAC=90°,设点B的横坐标为x,设点C的纵坐标为y,能表示y与x的函数关系的图象大致是( )
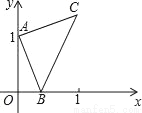
A. 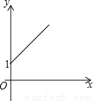 B.
B. 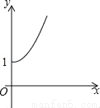 C.
C. 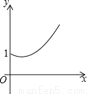 D.
D. 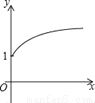
查看答案和解析>>
科目:初中数学 来源:2017年河北省中考数学模拟试卷 题型:单选题
若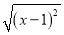 =1﹣x,则x的取值范围是( )
=1﹣x,则x的取值范围是( )
A. x>1 B. x≥1 C. x<1 D. x≤1
D 【解析】试题解析:由于二次根式的结果为非负数可知, 解得 故选D.查看答案和解析>>
科目:初中数学 来源:2017年陕西师大附中中考数学二模试卷 题型:解答题
计算: 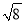 +
+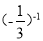 ﹣|2sin45°﹣1|.
﹣|2sin45°﹣1|.
查看答案和解析>>
科目:初中数学 来源:2017年湖北省武汉市中考数学模拟试卷 题型:解答题
已知x2+(a+3)x+a+1=0是关于x的一元二次方程.
(1)求证:方程总有两个不相等的实数根;
(2)若方程的两个实数根为x1 ,x2 ,且x12+x22=10,求实数a的值.
(1)证明见解析;(2)a的值为﹣2+ 或﹣2﹣. 【解析】【试题分析】 (1)欲证明方程总有两个不相等的实数根,只需证明根的判别式大于0即可. △=(a+3)2﹣4(a+1)=a2+6a+9﹣4a﹣4=a2+2a+5=(a+1)2+4>0,从而得证; (2)根据韦达定理,将x12+x22=10转化为两根之和与两根之积的形式,代入得到关于a的方程,从而求出a即可. x12+x22...查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com