
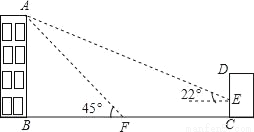
如图,某校教学楼AB的后面有一建筑物CD,当光线与地面的夹角是22°时,教学楼在建筑物的墙上留下高2米的影子CE;而当光线与地面夹角是45°时,教学楼顶A在地面上的影子F与墙角C有13米的距离(B、F、C在一条直线上)
(1)求教学楼AB的高度;
(2)学校要在A、E之间挂一些彩旗,请你求出A、E之间的距离(结果保留整数).
(参考数据:sin22°≈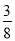 ,cos22°≈
,cos22°≈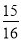 ,tan22°≈
,tan22°≈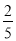 )
)
科目:初中数学 来源:青海省2017-2018学年七年级上学期12月月考数学试卷 题型:填空题
12am﹣1b3与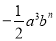 是同类项,则m+n=__________.
是同类项,则m+n=__________.
查看答案和解析>>
科目:初中数学 来源:江苏省东台市第三教育联盟2017-2018学年度第一学期第三次阶段检测七年级数学试卷 题型:解答题
如图,数轴上A,B两点对应的有理数分别为10和15,点P从点A出发,以每秒1个单位长度的速度沿数轴正方向运动,点Q同时从原点O出发,以每秒2个单位长度的速度沿数轴正方向运动,设运动时间为t秒.

(1)当0<t<5时,用含t的式子填空:
BP=_______,AQ=_______;
(2)当t=2时,求PQ的值;
(3)当PQ=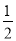 AB时,求t的值.
AB时,求t的值.
查看答案和解析>>
科目:初中数学 来源:江苏省东台市第三教育联盟2017-2018学年度第一学期第三次阶段检测七年级数学试卷 题型:填空题
多项式ab﹣2ab2﹣a的次数为________
3 【解析】试题分析:多项式的次数为其中一项的次数,这一项未知数的次数之和最高;根据定义可知多项式的次数为3次.查看答案和解析>>
科目:初中数学 来源:江苏省东台市第三教育联盟2017-2018学年度第一学期第三次阶段检测七年级数学试卷 题型:单选题
在下列各数:﹣3,+8,3.14,0,π, 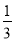 ,﹣0.4,2.75%,0.1010010001…中,有理数的个数是( )
,﹣0.4,2.75%,0.1010010001…中,有理数的个数是( )
A. 6个 B. 7个 C. 8个 D. 9个
B 【解析】试题分析:无理数是指无限不循环小数,根据定义可知:-3,+8,314,0, ,-0.4,275%是有理数,共7个,故选B.查看答案和解析>>
科目:初中数学 来源:2017年贵州省中考数学二模试卷 题型:填空题
(2010•沈阳)如图,在?ABCD中,点E在边BC上,BE:EC=1:2,连接AE交BD于点F,则△BFE的面积与△DFA的面积之比为 .
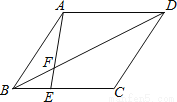
查看答案和解析>>
科目:初中数学 来源:2017年贵州省中考数学二模试卷 题型:单选题
已知反比例函数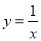 ,下列结论中不正确的是( )
,下列结论中不正确的是( )
A. 图象经过点(-1,-1) B. 图象在第一、三象限
C. 当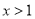 时,
时, 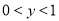 D. 当
D. 当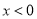 时,y随着x的增大而增大
时,y随着x的增大而增大
查看答案和解析>>
科目:初中数学 来源:黄金30题系列 九年级数学 大题易丢分 题型:解答题
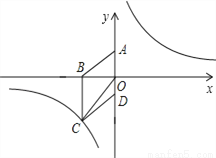
如图,在平面直角坐标系中,已知四边形ABCD为菱形,且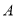 (0,3)、
(0,3)、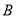 (﹣4,0).
(﹣4,0).
(1)求经过点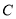 的反比例函数的解析式;
的反比例函数的解析式;
(2)设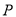 是(1)中所求函数图象上一点,以
是(1)中所求函数图象上一点,以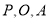 顶点的三角形的面积与△COD的面积相等.求点P的坐标.
顶点的三角形的面积与△COD的面积相等.求点P的坐标.
【答案】(1)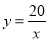 ;(2)P(
;(2)P(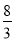 ,
, 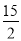 )或(-
)或(-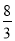 ,-
,-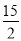 ).
).
【解析】试题分析:综合考查反比例函数及菱形的性质,注意:根据菱形的性质得到点C的坐标;点P的横坐标的有两种情况.
(1)根据菱形的性质可得菱形的边长,进而可得点C的坐标,代入反比例函数解析式可得所求的解析式; (2)设出点P的坐标,易得△COD的面积,利用点P的横坐标表示出△PAO的面积,那么可得点P的横坐标,就求得了点P的坐标.
试题解析:(1)由题意知,OA=3,OB=4,
在Rt△AOB中,AB=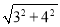 =5,
=5,
∵四边形ABCD为菱形,
∴AD=BC=AB=5,
∴C(-4,-5).
设经过点C的反比例函数的解析式为y=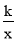 (k≠0),
(k≠0),
则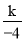 =-5,解得k=20.
=-5,解得k=20.
故所求的反比例函数的解析式为y=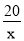 .
.
(2)设P(x,y),
∵AD=AB=5,OA=3,
∴OD=2,S△COD=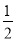 ×2×4=4,
×2×4=4,
即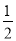 •OA•|x|=4,
•OA•|x|=4,
∴|x|=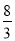 ,
,
∴x=±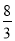 ,、
,、
当x=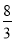 时,y=
时,y=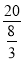 =
=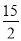 ,当x=-
,当x=-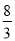 时,y=
时,y=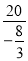 =-
=-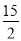 ,
,
∴P(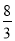 ,
, 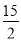 )或(?
)或(?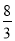 ,?
,?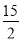 ).
).
考点:反比例函数综合题.
【题型】解答题
【结束】
14
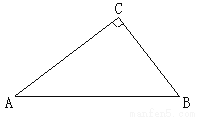
如图,在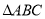 中,
中, 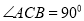 ,点
,点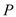 到
到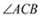 两边的距离相等,且
两边的距离相等,且 .
.
(1)先用尺规作出符合要求的点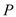 (保留作图痕迹,不需要写作法),然后判断△ABP的形状,并说明理由;
(保留作图痕迹,不需要写作法),然后判断△ABP的形状,并说明理由;
(2)设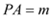 ,
,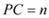 ,试用
,试用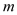 、
、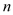 的代数式表示
的代数式表示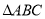 的周长和面积;
的周长和面积;
(3)设 与
与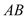 交于点
交于点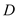 ,试探索当边
,试探索当边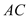 、
、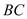 的长度变化时,
的长度变化时,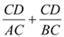 的值是否发生变化,若不变,试求出这个不变的值,若变化,试说明理由.
的值是否发生变化,若不变,试求出这个不变的值,若变化,试说明理由.
查看答案和解析>>
科目:初中数学 来源:黄金30题系列 七年级数学 小题易丢分 题型:单选题
按某种标准把多项式进行分类时,3x3﹣4和a2b+ab2+1属于同一类,则下列哪一个多项式也属于此类( )
A. abc﹣1 B. x2﹣2 C. 3x2+2xy4 D. m2+2mn+n2
A 【解析】从多项式的次数考虑求解. 【解析】 3x3﹣4和a2b+ab2+1属于同一类,都是3次多项式, A、abc﹣1是3次多项式,故本选项正确; B、x2﹣2是2次多项式,故本选项错误; C、3x2+2xy4是5次多项式,故本选项错误; D、m2+2mn+n2是2次多项式,故本选项错误. 故选A.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com