
(-6 x4 y7)÷ (-2 x y2) ÷(-3 x2y4)
- x y 【解析】试题分析:由单项式除以单项式法则与同底数幂的除法法则可完成此题 试题解析:(-6 x4 y7)÷ (-2 x y2) ÷(-3 x2y4)= - x4-1-2y7-2-4=- xy. 一线名师提优试卷系列答案
一线名师提优试卷系列答案 阳光试卷单元测试卷系列答案
阳光试卷单元测试卷系列答案科目:初中数学 来源:北师大版 七年级数学下册 第一章 整式的乘除 单项式与多项式相乘 专题练习题 含答案 题型:单选题
下列运算正确的是( )
A. -2x(3x2y-2xy)=6x3y-4x2y
B. 2xy2(-x2+2y2+1)=-4x3y4
C. (3ab2-2ab)·abc=2a3b4-2a2b2
D. (ab)2(2ab2-c)=2a3b4-a2b2c
D 【解析】试题分析:单项式乘以单项式,首先将系数进行相乘,然后根据同底数幂乘法计算法则进行计算得出答案.A、原式= ,计算错误;B、原式=,计算错误;C、原式= ,计算错误;D、计算正确,故本题选D.查看答案和解析>>
科目:初中数学 来源:江苏省苏州市张家港市2016-2017学年九年级(上)期末数学试卷 题型:解答题
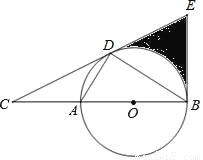
如图,D为⊙O上一点,点C在直径BA的延长线上,且∠CDA=∠CBD.
(1)求证:CD是⊙O的切线;
(2)过点B作⊙O的切线交CD的延长线于点E,CD=2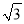 .
.
①若∠C=30°,求图中阴影部分的面积;
②若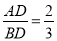 ,求BE的长.
,求BE的长.
查看答案和解析>>
科目:初中数学 来源:江苏省苏州市张家港市2016-2017学年九年级(上)期末数学试卷 题型:单选题
若点M(﹣1,y1),N(1,y2),P(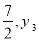 )都在抛物线y=﹣mx2+4mx+m2+1(m>0)上,则下列结论正确的是( )
)都在抛物线y=﹣mx2+4mx+m2+1(m>0)上,则下列结论正确的是( )
A. y1<y2<y3 B. y1<y3<y2 C. y3<y1<y2 D. 2<y1<y3
B 【解析】观察二次函数的图象可知:y1<y3<y2. 故选:B.查看答案和解析>>
科目:初中数学 来源:江苏省苏州市张家港市2016-2017学年九年级(上)期末数学试卷 题型:单选题
若2x=3y,则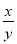 的值为( )
的值为( )
A. 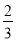 B.
B. 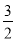 C.
C. 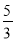 D.
D. 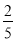
查看答案和解析>>
科目:初中数学 来源:北师大版数学七年级下册第一章整式乘法1.7整式的除法课时练习 题型:填空题
(2a3b2+8a2c)÷2a2等于_______;
ab2+4c 【解析】(2a3b2+8a2c)÷2a2=2a3b2÷2a2+8a2c÷2a2= ab2+4c, 故答案为:ab2+4c.查看答案和解析>>
科目:初中数学 来源:北师大版数学七年级下册第一章整式乘法1.7整式的除法课时练习 题型:单选题
(4x2y4+4x2z ) ÷(2x)2等于( )
A. 4y4+z B. -y4+z C. y4+x2z D. y4+z
D 【解析】(4x2y4+4x2z ) ÷(2x)2=(4x2y4+4x2z ) ÷4x2=4x2y4÷4x2+4x2z ÷4x2= y4+x2z, 故选:D.查看答案和解析>>
科目:初中数学 来源:北师大版七年级数学下3.1 用表格表示的变量间关系 同步练习 题型:单选题
一个圆柱的高h为10 cm,当圆柱的底面半径r由小到大变化时,圆柱的体积V也发生了变化,在这个变化过程中( )
A. r是因变量,V是自变量 B. r是自变量,V是因变量
C. r是自变量,h是因变量 D. h是自变量,V是因变量
B 【解析】圆柱的高h=10厘米,因此h是常量不是变量,故排除C、D,圆柱的体积V随底面圆半径r的变化而变化,所以r是自变量,V是因变量. 故答案为:B.查看答案和解析>>
科目:初中数学 来源:北师大版七年级数学下册 第二章 相交线与平行线 2.2 探索直线平行的条件 同位角及平行公理 同步课堂练习题 题型:解答题
如图,三角形ABC中,已知∠C=45°,∠ADB=90°,DE为∠ADB的平分线,DE与CA平行吗?说明你的理由.
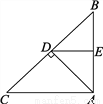
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com