
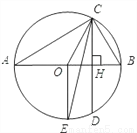
如图所示,AB为⊙O的直径,CD为弦,且CD⊥AB,垂足为H.
(1)如果⊙O的半径为4,CD=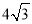 ,求∠BAC的度数;
,求∠BAC的度数;
(2)若点E为弧ADB的中点,连接OE,CE.求证:CE平分∠OCD.
科目:初中数学 来源:山西省2017-2018学年八年级上期末模拟数学试卷 题型:填空题
在实数范围内因式分【解析】
x3﹣2x2y+xy2=________.
查看答案和解析>>
科目:初中数学 来源:2016-2017学年黑龙江省哈尔滨市松北区2017届九年级上学期期末数学试卷 题型:单选题
如图所示的由六个小正方体组成的几何体的俯视图是( )
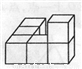
A. 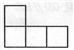 B.
B. 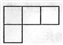 C.
C. 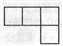 D.
D. 
查看答案和解析>>
科目:初中数学 来源:黑龙江省密山市2017-2018学年八年级上学期期中考试数学试卷 题型:填空题
若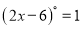 ,则x应满足的条件是____________。
,则x应满足的条件是____________。
查看答案和解析>>
科目:初中数学 来源:黑龙江省密山市2017-2018学年八年级上学期期中考试数学试卷 题型:单选题
等腰三角形两边长分别为4和8,则这个等腰三角形的周长为( )
A. 16 B. 18 C. 20 D. 16或20
C 【解析】试题分析:由于题中没有指明哪边是底哪边是腰,则应该分两种情况进行分析. ①当4为腰时,4+4=8,故此种情况不存在; ②当8为腰时,8-4<8<8+4,符合题意. 故此三角形的周长=8+8+4=20. 故选D查看答案和解析>>
科目:初中数学 来源:2017-2018学年第一学期期末复习备考之精准复习模拟题九年级人教版数学试卷(C卷) 题型:解答题
已知关于x的一元二次方程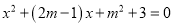 有两个不相等的实数根,求m的取值范围.
有两个不相等的实数根,求m的取值范围.
查看答案和解析>>
科目:初中数学 来源:2017-2018学年第一学期期末复习备考之精准复习模拟题九年级人教版数学试卷(C卷) 题型:填空题
如图,将边长为(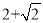 )cm的正方形绕其中心旋转45°,则两个正方形公共部分(图中阴影部分)的面积为___________cm2.
)cm的正方形绕其中心旋转45°,则两个正方形公共部分(图中阴影部分)的面积为___________cm2.
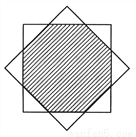
查看答案和解析>>
科目:初中数学 来源:2017-2018学年第一学期期末复习备考之精准复习模拟题九年级人教版数学试卷(A卷) 题型:解答题
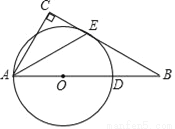
如图,Rt△ABC,∠C=90°,点D为AB上的一点,以AD为直径的⊙O与BC相切于点E,连接AE.
(1)求证:AE平分∠BAC;
(2)若AC=8,OB=18,求BD的长.
查看答案和解析>>
科目:初中数学 来源:河南省2017-2018学年八年级(上)第一次月考数学试卷 题型:单选题
如图,E,B,F,C四点在一条直线上,EB=CF,∠A=∠D,再添一个条件仍不能证明△ABC≌△DEF的是( )
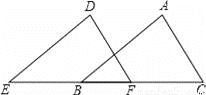
A. AB=DE B. DF∥AC
C. ∠E=∠ABC D. AB∥DE
A 【解析】由EB=CF,可得出EF=BC,又有∠A=∠D,本题具备了一组边、一组角对应相等,为了再添一个条件仍不能证明△ABC≌△DEF,那么添加的条件与原来的条件可形成SSA,就不能证明△ABC≌△DEF了. 【解析】 添加选项A中的DE=AB与原条件满足SSA,不能证明△ABC≌△DEF. 添加选项B中的DF∥AC,可得∠DFE=∠ACB,根据AAS能证明△ABC≌△DE...查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com