
如图,等腰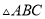 三个顶点在⊙
三个顶点在⊙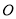 上,直径
上,直径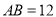 ,
, 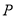 为弧
为弧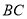 上任意一点(不与
上任意一点(不与 ,
, 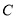 重合),直线
重合),直线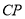 交
交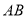 延长线于点
延长线于点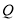 ,
, 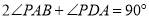 ,下列结论正确的是( ).
,下列结论正确的是( ).
①若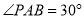 ,则弧
,则弧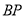 的长为
的长为 ;②若
;②若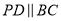 ,则
,则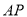 平分
平分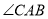 ;
;
③若 ,则
,则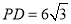 ;④无论点
;④无论点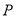 在弧
在弧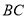 上的位置如何变化,
上的位置如何变化, 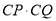 为定值.
为定值.

A. ②③ B. ②③④ C. ①③④ D. ②④
B 【解析】如图,连接, ①∵, , ∴, 又, , ∴弧的长为,故①错误. ②∵, ∴, 又是直径, ∴, ∴, ∵, ∴, ∴,即平分,故②正确. ③∵, ∴, 在中, ,即, 又, ∴, ∴, ∴是等边三角形, , ∴, ∴在中, .故③正确. ④在⊙中,... 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源:人教版七年级下册数学第7-10章综合测试卷 题型:解答题
若不等式组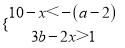 的解集为﹣2<x<4,求出a、b的值.
的解集为﹣2<x<4,求出a、b的值.
查看答案和解析>>
科目:初中数学 来源:人教版七年级下册数学第6章实数单元检测卷 题型:单选题
下列说法正确的是( )
A. (﹣3)2的算术平方根是3 B. 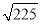 的平方根是±15
的平方根是±15
C. 当x=0或2时, 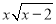 =0 D.
=0 D. 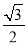 是分数
是分数
查看答案和解析>>
科目:初中数学 来源:浙江杭州西湖区公益中学2018届九年级上学期期中数学试卷 题型:解答题
如图,圆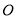 的直径为
的直径为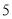 ,在圆
,在圆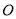 上位于直径
上位于直径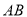 的异侧有定点
的异侧有定点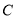 和动点
和动点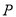 ,已知
,已知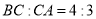 ,点
,点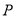 在半圆弧
在半圆弧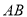 上运动(不与
上运动(不与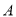 、
、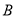 重合),过
重合),过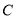 作
作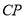 的垂线
的垂线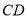 交
交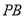 的延长线于
的延长线于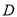 点.
点.
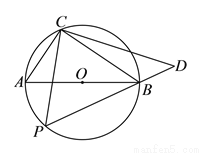
( )求证:
)求证: 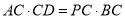 .
.
( )当点
)当点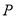 运动到
运动到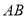 弧中点时,求
弧中点时,求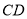 的长.
的长.
(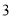 )当点
)当点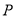 运动到什么位置时,
运动到什么位置时, 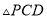 的面积最大?并求这个最大面积
的面积最大?并求这个最大面积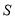 .
.
查看答案和解析>>
科目:初中数学 来源:浙江杭州西湖区公益中学2018届九年级上学期期中数学试卷 题型:填空题
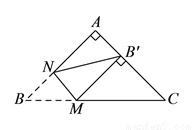
如图,在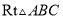 中,
中,  ,
,  ,
,  ,点
,点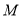 ,
, 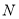 分别是边
分别是边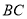 ,
,  上的动点,沿
上的动点,沿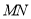 所在的直线折叠
所在的直线折叠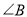 ,使点
,使点 的对应点
的对应点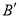 始终落在边
始终落在边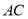 上,若
上,若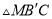 为直角三角形,则
为直角三角形,则 的长为__________.
的长为__________.
查看答案和解析>>
科目:初中数学 来源:浙江杭州西湖区公益中学2018届九年级上学期期中数学试卷 题型:单选题
如图,点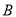 在线段
在线段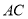 上,且
上,且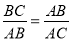 ,设
,设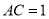 ,则
,则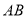 的长是( ).
的长是( ).
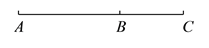
A. 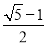 B.
B. 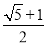 C.
C. 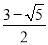 D.
D. 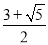
查看答案和解析>>
科目:初中数学 来源:北师大版九年级下册数学第一章直角三角形的边角关系单元检测卷 题型:解答题
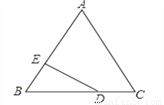
如图,D为等边△ABC边BC上一点,DE⊥AB于E,若BD:CD=2:1,DE=2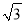 , 求AE.
, 求AE.
查看答案和解析>>
科目:初中数学 来源:北师大版九年级下册数学第一章直角三角形的边角关系单元检测卷 题型:单选题
如图,在平面直角坐标系中,直线OA过点(2,1),则tanα的值是( )
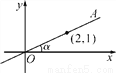
A. 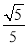 B.
B. 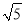 C.
C. 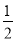 D. 2
D. 2
查看答案和解析>>
科目:初中数学 来源:北师大版七年级下册 第一章 整式的乘除 1.3同底数幂的除法 同步测试 题型:单选题
(-2)0的值为( )
A. -2 B. 0 C. 1 D. 2
C 【解析】试题解析: 故选C.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com