
如图,AB是⊙O的直径,CD是弦,∠ABC=65°,则∠D的度数为( )
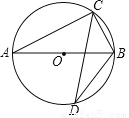
A. 130° B. 65° C. 35° D. 25°
D 【解析】试题分析:先根据圆周角定理得出∠ACB=90°,∠A=∠D,再由∠ABC=65°可得出∠A的度数,进而可得出结论. 【解析】 ∵AB是O的直径, ∴∠ACB=90°. ∵∠ABC=65°, ∴∠D=∠A=90°?65°=25°. 故选D. 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源:人教版九年级上册数学 23.2.3关于原点对称的点的坐标 测试 题型:单选题
已知点P(2+m,n﹣3)与点Q(m,1+n)关于原点对称,则m﹣n的值是( )
A.1 B.﹣1 C.2 D.﹣2
D 【解析】 试题分析:根据关于原点对称的点的横坐标互为相反数,纵坐标互为相反数,可得m、n的值,根据有理数的减法,可得答案. 【解析】 由点P(2+m,n﹣3)与点Q(m,1+n)关于原点对称,得 2+m+m=0,n﹣3+1+n=0. 解得m=﹣1,n=1. m﹣n=﹣1﹣1=﹣2, 故选:D.查看答案和解析>>
科目:初中数学 来源:人教版九年级上册 22.3 二次函数的应用 同步测试 题型:单选题
用长为6m的铝合金型材做一个形状如图所示的矩形窗框,要使做成的窗框的透光面积最大,则该窗的长,宽应分别做成( )

A. 1.5m,1m B. 1m,0.5m C. 2m,1m D. 2m,0.5m
A 【解析】试题分析:设长为x,则宽为,S=,即S=, 要使做成的窗框的透光面积最大,则x=,于是宽为=1m, 所以要使做成的窗框的透光面积最大,则该窗的长,宽应分别做成1.5m,1m,故选A.查看答案和解析>>
科目:初中数学 来源:山东省聊城市2018届九年级上学期期中考试数学试卷 题型:填空题
已知一个正六边形的边心距为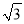 ,则它的半径为______ .
,则它的半径为______ .
查看答案和解析>>
科目:初中数学 来源:山东省聊城市2018届九年级上学期期中考试数学试卷 题型:单选题
如图,一艘潜艇在海面下500米A处测得俯角为30°的海底C处有一黑匣子发出信号,继续在同一深度直线航行4000米后,在B处测得俯角为60°的海底也有该黑匣子发出的信号,则黑匣子所在位置点C在海面下的深度为( )
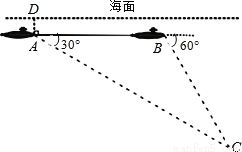
A. 2000米 B. 4000米 C. 2000米 D. (2000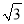 +500)米
+500)米
查看答案和解析>>
科目:初中数学 来源:北师大版数学七年级上册5.3应用一元一次方程--水箱变高了课时练习(含解析) 题型:解答题
A、B两站相距300千米,一列快车从A站开出,行驶速度是每小时60千米,一列慢车从B站开出,行驶速度是每小时40千米,快车先开15分钟,两车相向而行,快车开出几小时后两车相遇?(只列出方程,不用解)
. 【解析】试题分析:等量关系:快车行驶的路程+慢车行驶的路程=两车相距的路程,设快车开出x小时后两车相遇,快车行驶的路程为:60x千米,慢车行驶的路程为:40(x-)千米,根据题意可列出方程. 试题解析:设快车开出x小时后两车相遇, 根据题意得: .查看答案和解析>>
科目:初中数学 来源:北师大版数学七年级上册5.3应用一元一次方程--水箱变高了课时练习(含解析) 题型:填空题
某工厂生产一种零件,计划在20天内完成,若每天多生产4个,则15天完成且还多生产10个.设原计划每天生产x个,根据题意可列方程为______.
20x=15(x+4)-10. 【解析】根据等量关系:实际15天完成的数量比计划20天完成的数量多10个,设原计划每天生产x个,原计划20天生产数量为:20x,实际15天生产的数量为:15(x+4),根据题意可列出方程为: 20x=15(x+4)-10,故答案为: 20x=15(x+4)-10.查看答案和解析>>
科目:初中数学 来源:人教版九年级上册数学 第23章小结与复习 测试 题型:解答题
如图,已知四边形ABCD及点O.求作:四边形A′B′C′D′,使得四边形 与四边形ABCD关于O点中心对称
与四边形ABCD关于O点中心对称
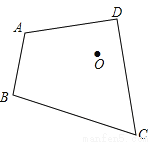
查看答案和解析>>
科目:初中数学 来源:人教版九年级上册数学 22.3实际问题与二次函数(3)测试 题型:单选题
小敏在今年的校运动会跳远比赛中跳出了满意一跳,函数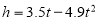 (的单位:秒,
(的单位:秒,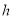 的单位:米)可以描述他跳跃时重心高度的变化,则他起跳后到重心最高时所用的时间是( )
的单位:米)可以描述他跳跃时重心高度的变化,则他起跳后到重心最高时所用的时间是( )
A.0.71s B.0.70s C.0.63s D.0.36s
D 【解析】 试题分析:二次函数可配方成 .当,重心最高.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com