
某物流公司的甲、乙两辆货车分别从相距300千米的A、B两地同时出发相向而行,并以各自的速度匀速行驶,两车行驶1.5小时时甲车先到达配货站C地,此时两车相距30千米,甲车在C地用1小时配货,然后按原速度开往B地;乙车行驶2小时时也到C地,未停留继续开往A地。(友情提醒:画出线段图帮助分析)
(1)乙车的速度是 千米/小时,B、C两地的距离是 千米,A、C两地的距离是 千米;
(2)求甲车的速度及甲车到达B地所用的时间;
(3)乙车出发多长时间,两车相距150千米.
(1)60;120;180;(2)120;3.5;(3)小时或小时. 【解析】试题分析:(1)由题意可知,甲车2小时到达C地,休息了20分钟,乙车行驶2小时15分钟也到C地,这15分钟甲车未动,即乙车15分钟走了20千米,据此可求出乙车的速度,再根据速度求出B、C两地的距离和A、C两地的距离即可解答. (2)根据A、C两地的距离和甲车到达配货站C地的时间可求出甲车的速度,再根据行程问题...科目:初中数学 来源:2018春季学北师大版九年级数学下册期末测评试卷 题型:解答题
已知点A(-2,n)在抛物线y=x2+bx+c上.
(1)若b=1,c=3,求n的值;
(2)若此抛物线经过点B(4,n),且二次函数y=x2+bx+c的最小值是-4,请画出点P(x-1,x2+bx+c)的纵坐标随横坐标变化的图象,并说明理由.
(1)5;(2)作图见解析. 【解析】试题分析:(1)代入,以及点的坐标即可求得的值; (2)根据题意求得抛物线的解析式为从而求得点P(x-1,x2+bx+c)的纵坐标随横坐标变化的关系式为y=x'2-4,然后利用5点式画出函数的图象即可. 试题解析: (1) b=1,c=3,∴y=x2+x+3. 点A(-2,n)在抛物线y=x2+bx+c上, n=4-2+3=5....查看答案和解析>>
科目:初中数学 来源:宁夏2017-2018学年度上期七年级数学期末综合检测模拟试卷 题型:单选题
下列适合普查的是( )
A. 调查郑州市的空气质量 B. 调查一批炸弹的杀伤范围
C. 调查河南人民的生活幸福指数 D. 调查全班同学对电视节目“梨园春”的知晓率
D 【解析】试题解析:A、调查郑州市的空气质量,全面调查无法做到,故此选项错误; B、调查一批炸弹的杀伤范围,全面调查难度较大,故此选项错误; C、调查河南人民的生活幸福指数,全面调查难度较大,故此选项错误; D、调查全班同学对电视节目“梨园春”的知晓率,人数较少,适合抽样调查. 故选D.查看答案和解析>>
科目:初中数学 来源:吉林省2018届九年级(上)期中数学试卷 题型:单选题
如图所示,函数y=ax2(a≠0)和y=﹣ax+b(a≠0)在同一坐标系中的图象可能为( )
A. 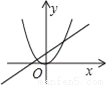 B.
B. 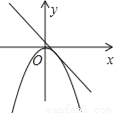 C.
C. 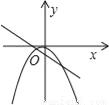 D.
D. 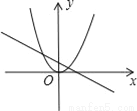
查看答案和解析>>
科目:初中数学 来源:2017年四川省数学七年级(上)期末数学试卷 题型:解答题
(1)化简后再求值: 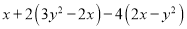 ,其中
,其中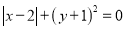
(2)若关于x、y的单项式cx2a+2y2与0.4xy3b+4的和为零,则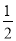 a2b-[
a2b-[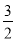 a2b-(3abc-a2c)-4a2c]-3abc的值又是多少?
a2b-(3abc-a2c)-4a2c]-3abc的值又是多少?
查看答案和解析>>
科目:初中数学 来源:2017年四川省数学七年级(上)期末数学试卷 题型:填空题
若单项式2x2ym与-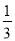 xny3是同类项,则m+n的值是__________;
xny3是同类项,则m+n的值是__________;
查看答案和解析>>
科目:初中数学 来源:辽宁省2017-2018学年八年级上学期期末考试数学试卷 题型:解答题
如图,(1)在图中画出△ABC关于y轴对称的图形△A1B1C1;
(2)在x轴上找出一点P, 使得点P到点A、点B的距离之和最短(保留作图痕迹)
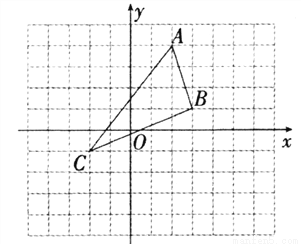
查看答案和解析>>
科目:初中数学 来源:贵州省2017-2018学年七年级(上)期中数学试卷 题型:单选题
若|x|=2,|y|=3,则|x+y|的值为( )
A. 5 B. ﹣5 C. 5或1 D. 以上都不对
C 【解析】∵|x|=2,|y|=3, ∴x=2或-2,y=3或-3, 当x=2,y=3时,│x+y│=5; 当x=-2,y=3时,│x+y│=1; 当x=-2,y=-3时,│x+y│=5; 当x=-2,y=3时,│x+y│=1; 所以|x+y|的值是1或5. 故选C.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com