已知点A在抛物线y=x2+bx+c上.(1)若b=1,c=3,求n的值;(2)若此抛物线经过点B(4,n),且二次函数y=x2+bx+c的最小值是-4,请画出点P的纵坐标随横坐标变化的图象,并说明理由. 作图见解析. [解析]试题分析:(1)代入.以及点的坐标即可求得的值, (2)根据题意求得抛物线的解析式为从而求得点P的纵坐标随横坐标变化的关系式为y=x'2-4, 题目和参考答案——青夏教育精英家教网—

已知点A(-2,n)在抛物线y=x2+bx+c上.

(1)若b=1,c=3,求n的值;

(2)若此抛物线经过点B(4,n),且二次函数y=x2+bx+c的最小值是-4,请画出点P(x-1,x2+bx+c)的纵坐标随横坐标变化的图象,并说明理由.

(1)5;(2)作图见解析. 【解析】试题分析：（1）代入，以及点的坐标即可求得的值；（2）根据题意求得抛物线的解析式为从而求得点P(x-1,x2+bx+c)的纵坐标随横坐标变化的关系式为y=x'2-4,然后利用5点式画出函数的图象即可．试题解析： (1) b=1,c=3,∴y=x2+x+3. 点A(-2,n)在抛物线y=x2+bx+c上, n=4-2+3=5....

练习册系列答案

年级	高中课程	年级	初中课程
高一	高一免费课程推荐！	初一	初一免费课程推荐！
高二	高二免费课程推荐！	初二	初二免费课程推荐！
高三	高三免费课程推荐！	初三	初三免费课程推荐！
更多初中、高中辅导课程推荐,点击进入>>

相关习题

科目：初中数学 来源：湖北省大冶市金湖街办2017-2018学年八年级上学期第二次月考（12月）数学试卷 题型：解答题

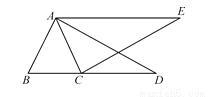
如图，在△ABC中，∠ABC＝∠ACB，过A作AD⊥AB交BC的延长线于点D，过点C作CE⊥AC，使AE＝BD．求证：∠E＝∠D．

证明见解析．【解析】试题分析：利用已知条件证明Rt△BAD≌Rt△ACE，根据全等三角形的对应角相等即可解答．试题解析：【解析】 ∵∠ABC=∠ACB，∴AB=AC．∵AD⊥AB，CE⊥AC，∴∠BAD=∠ACE=90°．在Rt△BAD和Rt△ACE中，∵AE=BD，AB=AC，∴Rt△BAD≌Rt△ACE，∴∠E=∠D．

查看答案和解析>>

科目：初中数学 来源：辽宁省2017-2018学年七年级上学期期末考试数学试卷 题型：单选题

解方程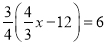，下列解法中，较为简便的是（）

A. 两边都乘以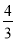，得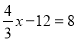 B. 两边都乘以4，得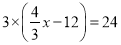

C. 用分配律去括号，得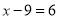 D. 小括号内先通分，得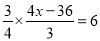

C 【解析】【解析】方程解法较为简便的是去括号得：x﹣9=6．故选C．

查看答案和解析>>

科目：初中数学 来源：浙江省湖州市吴兴区2017-2018学年九年级上学期期末考试数学试卷 题型：单选题

在平面直角坐标系中，我们把横、纵坐标都是整数的点叫做整点.如图，已知⊙O的半径为5，则抛物线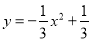与该圆所围成的阴影部分（不包括边界）的整点个数是（）

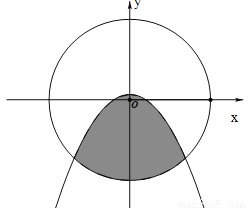
A. 24 B. 23 C. 22 D. 21

D 【解析】∵抛物线顶点坐标为（0，），半径为5的⊙O与y轴负半轴交点为（0，-5）， ∴当y=0时，x=±1，∴整点为（1，0），（0，0），（-1，0）；当y=-1，x=±2，∴整点为（2，-1），（-1，-1），（0，-1），（1，-1），（2，-1）；当y=-2，x=±，∴整点为（2，-2），（-1，-2），（0，-2），（1，-2），（2，-2）； ...

查看答案和解析>>

科目：初中数学 来源：浙江省湖州市吴兴区2017-2018学年九年级上学期期末考试数学试卷 题型：单选题

抛物线y=2(x+4)2-3的对称轴是 ( )

A. 直线x=4 B. 直线x=－4 C. 直线x=3 D. 直线x=－3

B 【解析】抛物线的顶点式方程为y=a（x-h）2+k，顶点坐标是（h，k），对称轴是x=h，所以抛物线y=2（x+4）2-3的对称轴是x=-4；故选：B．

查看答案和解析>>

科目：初中数学 来源：2018春季学北师大版九年级数学下册期末测评试卷 题型：填空题

如图,已知点A从点(1,0)出发,以每秒1个单位长度的速度沿着x轴的正方向运动,经过t s后,以O,A为顶点作菱形OABC,使点B,C都在第一象限内,且∠AOC=60°,又以点P(0,4)为圆心,PC为半径的圆恰好与OA所在的直线相切,则t=_____.

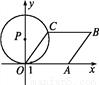
【解析】试题解析：由题意可知,当以点P(0,4)为圆心,PC为半径的圆恰好与OA所在的直线相切时,如图. 连接PC,作PD⊥OC于点D,则 ∴OD=OP=×4=2. ∴OC=2OD=4, ∴OA=OC=4,则t=4-1. 故答案为： .

查看答案和解析>>

科目：初中数学 来源：2018春季学北师大版九年级数学下册期末测评试卷 题型：单选题

如果一个扇形的弧长等于它的半径,那么此扇形称为“等边扇形”.则半径为2的“等边扇形”的面积为(　　)

A. π B. 1 C. 2 D.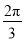

C 【解析】试题解析：由扇形面积公式,得“等边扇形”的面积为×2×2=2, 故选C.

查看答案和解析>>

科目：初中数学 来源：宁夏2017-2018学年度上期七年级数学期末综合检测模拟试卷 题型：填空题

已知三角形的第一边长是a+2b，第二边比第一边长(b - 2)，第三边比第二边短5，则三角形的周长为__.

3a+8b – 9 【解析】试题解析：三角形的周长为a+2b+a+2b+b-2+a+2b+b-2-5=3a+8b-9. 故答案为：3a+8b-9．

查看答案和解析>>

科目：初中数学 来源：2017年四川省数学七年级（上）期末数学试卷 题型：解答题

某物流公司的甲、乙两辆货车分别从相距300千米的A、B两地同时出发相向而行，并以各自的速度匀速行驶，两车行驶1.5小时时甲车先到达配货站C地，此时两车相距30千米，甲车在C地用1小时配货，然后按原速度开往B地；乙车行驶2小时时也到C地，未停留继续开往A地。（友情提醒：画出线段图帮助分析）

（1）乙车的速度是千米/小时，B、C两地的距离是千米，A、C两地的距离是千米；

（2）求甲车的速度及甲车到达B地所用的时间；

（3）乙车出发多长时间，两车相距150千米.

（1）60；120；180；（2）120；3.5；（3）小时或小时. 【解析】试题分析：（1）由题意可知，甲车2小时到达C地，休息了20分钟，乙车行驶2小时15分钟也到C地，这15分钟甲车未动，即乙车15分钟走了20千米，据此可求出乙车的速度，再根据速度求出B、C两地的距离和A、C两地的距离即可解答．（2）根据A、C两地的距离和甲车到达配货站C地的时间可求出甲车的速度，再根据行程问题...

查看答案和解析>>

同步练习册答案

练习册

高中

初中

小学