
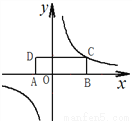
如图,长方形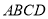 中,边
中,边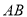 在
在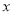 轴上(点
轴上(点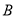 在
在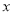 轴的正半轴上),
轴的正半轴上), 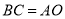 ,
, 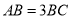 ,已知
,已知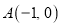 ,反比例函数
,反比例函数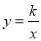 的图像经过点
的图像经过点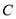 .
.
求:点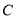 的坐标和反比例函数的解析式.
的坐标和反比例函数的解析式.
科目:初中数学 来源:黄金30题系列 七年级数学 小题好拿分 题型:单选题
如果x=6是方程2x+3a=6x的解,那么a的值是( )
A. 4 B. 8 C. 9 D. -8
B 【解析】试题解析:把x=6代入2x+3a=6x得: 2×6+3a=6×6, 解得:a=8. 故选B.查看答案和解析>>
科目:初中数学 来源:2017年辽宁省中考数学二模试卷 题型:解答题
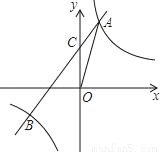
如图,反比例函数y=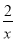 的图象与一次函数y=kx+b的图象交于点A(m,2),点B(﹣2,n ),一次函数图象与y轴的交点为C.
的图象与一次函数y=kx+b的图象交于点A(m,2),点B(﹣2,n ),一次函数图象与y轴的交点为C.
(1)求一次函数解析式;
(2)求C点的坐标;
(3)求△AOB的面积.
查看答案和解析>>
科目:初中数学 来源:2017年辽宁省中考数学二模试卷 题型:单选题
如图,点A是双曲线y=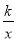 在第二象限分支上的任意一点,点B、点C、点D分别是点A关于x轴、坐标原点、y轴的对称点.若四边形ABCD的面积是8,则k的值为( )
在第二象限分支上的任意一点,点B、点C、点D分别是点A关于x轴、坐标原点、y轴的对称点.若四边形ABCD的面积是8,则k的值为( )
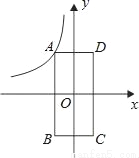
A. ﹣1 B. 1 C. 2 D. ﹣2
D 【解析】∵点B、点C、点D分别是点A关于x轴、坐标原点、y轴的对称点,∴四边形ABCD是矩形。∵四边形ABCD的面积是8,∴4×|-k|=8,解得|k|=2。 又∵双曲线位于第二、四象限,∴k<0。∴k=-2。故选D。查看答案和解析>>
科目:初中数学 来源:上海市2016-2017学年度第一学期八年级期末考试试卷 题型:解答题
已知,点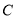 是线段
是线段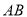 所在平面内任意一点,分别以
所在平面内任意一点,分别以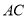 、
、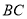 为边,在
为边,在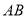 同侧作等边
同侧作等边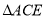 和等边
和等边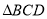 ,联结
,联结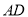 、
、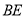 交于点
交于点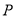 .
.
(1)如图1,当点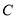 在线段
在线段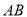 上移动时,线段
上移动时,线段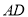 与
与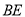 的数量关系是:________;
的数量关系是:________;
(2)如图2,当点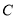 在直线
在直线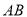 外,且
外,且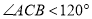 ,仍分别以
,仍分别以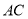 、
、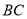 为边,在
为边,在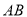 同侧作等边
同侧作等边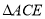 和等边
和等边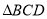 ,联结
,联结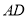 、
、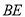 交于点
交于点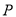 .(1)的结论是否还存在?若成立,请证明;若不成立,请说明理由.此时
.(1)的结论是否还存在?若成立,请证明;若不成立,请说明理由.此时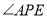 是否随
是否随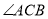 的大小发生变化?若变化,写出变化规律,若不变,请求出
的大小发生变化?若变化,写出变化规律,若不变,请求出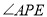 的度数;
的度数;
(3)如图3,在(2)的条件下,联结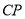 ,求证:
,求证: 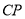 平分
平分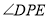 .
.

查看答案和解析>>
科目:初中数学 来源:上海市2016-2017学年度第一学期八年级期末考试试卷 题型:填空题
在直角坐标平面内的两点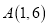 、
、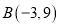 ,那么
,那么 、
、 两点的距离等于______.
两点的距离等于______.
查看答案和解析>>
科目:初中数学 来源:上海市2016-2017学年度第一学期八年级期末考试试卷 题型:填空题
在实数范围内分解因式: 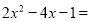 _____________.
_____________.
查看答案和解析>>
科目:初中数学 来源:重庆市江津区2016-2017学年七年级下学期期末考试数学试卷 题型:解答题
解下列方程:
(1)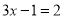
(2)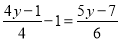
查看答案和解析>>
科目:初中数学 来源:2016-2017学年山西农业大学附中七年级(下)第二次月考数学试卷 题型:单选题
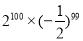 =
=
A、2 B、-2 C、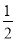 D、-
D、-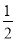
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com