
在双曲线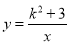 上有三个点A(x1,y1),B(x2,y2),C(x3,y3),若x1<x2<0<x3,则y1,y2 ,y3的大小关系是______________.(用“<”连接)
上有三个点A(x1,y1),B(x2,y2),C(x3,y3),若x1<x2<0<x3,则y1,y2 ,y3的大小关系是______________.(用“<”连接)
科目:初中数学 来源:北京海淀区2017-2018学年初二第一学期数学期末试卷 题型:单选题
若分式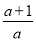 的值等于0,则
的值等于0,则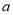 的值为( )
的值为( )
A. 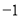 B. 1 C.
B. 1 C. 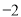 D. 2
D. 2
查看答案和解析>>
科目:初中数学 来源:江苏省2017-2018学年七年级12月月考数学试卷 题型:填空题
用一个平面截长方体、五棱柱、圆柱和圆锥,不能截出三角形的是________.
圆柱 【解析】当截面的角度和方向不同时,圆柱体的截面无论什么方向截取,都不会截得三角形. 【解析】 长方体沿体面对角线截几何体可以截出三角形; 五棱柱沿顶点截几何体可以截得三角形; 圆柱不能截出三角形; 圆锥沿顶点可以截出三角形. 故不能截出三角形的几何体是圆柱. 故答案为:圆柱.查看答案和解析>>
科目:初中数学 来源:福建省2017-2018学年九年级数学上学期期末检测试卷 题型:解答题
如图,已知抛物线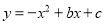 与
与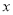 轴、
轴、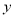 轴分别相交于点A(-1,0)和B(0,3),其顶点为D.
轴分别相交于点A(-1,0)和B(0,3),其顶点为D.
(1)求这条抛物线的解析式;
(2)若抛物线与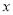 轴的另一个交点为E,求△ODE的面积;抛物线的对称轴上是否存在点P使得△PAB的周长最短.若存在请求出点P的坐标,若不存在说明理由.
轴的另一个交点为E,求△ODE的面积;抛物线的对称轴上是否存在点P使得△PAB的周长最短.若存在请求出点P的坐标,若不存在说明理由.
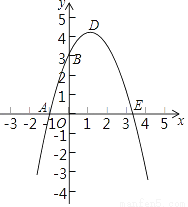
查看答案和解析>>
科目:初中数学 来源:福建省2017-2018学年九年级数学上学期期末检测试卷 题型:解答题
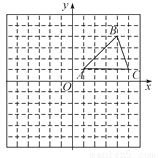
在平面直角坐标系中,△ABC的位置如图所示(每个小方格都是边长为1个单位长度的正方形).
(1)将△ABC沿x轴方向向左平移6个单位长度,画出平移后得到的△A1B1C1;
(2)将△ABC绕着点A顺时针旋转90°,画出旋转后得到的△AB2C2;
(3)直接写出点B2,C2的坐标.
查看答案和解析>>
科目:初中数学 来源:福建省2017-2018学年九年级数学上学期期末检测试卷 题型:单选题
如图,⊙O是△ABC的外接圆,已知∠ABO=50°,则∠ACB的大小为( )
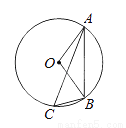
A. 40° B. 30° C. 45° D. 50°
A 【解析】试题解析:△AOB中,OA=OB,∠ABO=40°; ∴∠AOB=180°-2∠ABO=100°; ∴∠ACB=∠AOB=×100°=50°. 故选D.查看答案和解析>>
科目:初中数学 来源:福建省2017-2018学年九年级数学上学期期末检测试卷 题型:单选题
如果矩形的面积为6,那么它的长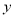 与宽
与宽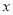 的函数关系用图象表示为( )
的函数关系用图象表示为( )
A. 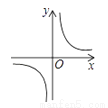 B.
B. 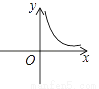 C.
C. 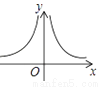 D.
D. 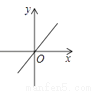
查看答案和解析>>
科目:初中数学 来源:湖北省武汉市青山区2017-2018学年七年级(上)期中数学试卷 题型:单选题
按照一定规律排列的n个数:﹣2、4、﹣8、16、﹣32、64、…,若最后三个数的和为768,则n为( )
A. 9 B. 10 C. 11 D. 12
B 【解析】试题解析:由题意,得第n个数为(﹣2)n, 那么(﹣2)n﹣2+(﹣2)n﹣1+(﹣2)n=768, 当n为偶数:整理得出:3×2n﹣2=768,解得:n=10; 当n为奇数:整理得出:﹣3×2n﹣2=768,则求不出整数, 故选B.查看答案和解析>>
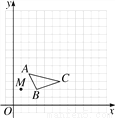
科目:初中数学 来源:江苏省南通市2018届九年级上学期第三次月考数学试卷 题型:解答题
在13×13的网格图中,已知△ABC和点M(1,2).
(1)以点M为位似中心,画出△ABC的位似图形△A′B′C′,其中△A′B′C′与△ABC的位似比为2;
(2)写出△A′B′C′的各顶点坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com