练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

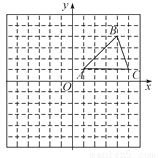
    在平面直角坐标系中，△ABC的位置如图所示（每个小方格都是边长为1个单位长度的正方形）．

    （1）将△ABC沿x轴方向向左平移6个单位长度，画出平移后得到的△A1B1C1；

    （2）将△ABC绕着点A顺时针旋转90°，画出旋转后得到的△AB2C2；

    （3）直接写出点B2，C2的坐标．

    （1）答案见解析；（2）答案见解析；（3）点B2（4，－2），C2（1，－3）． 【解析】试题分析：（1）利用点平移的规律写出点A、B、C的对应点A1、B1、C1的坐标，然后描点即可得到△A1B1C1； （2）利用网格特点和旋转的性质画出点B、C的对应点B2、C2，从而得到△AB2C2，再写出点B2、C2的坐标． 试题解析：【解析】 （1）如图，△A1B1C1即为所求； ...
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源：北京海淀区2017-2018学年初二第一学期数学期末试卷 题型：单选题

    若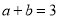，则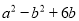的值为（ ）

    A. 3 B. 6 C. 9 D. 12

    C 【解析】∵a+b=3， ∴a2-b2+6b=(a+b)(a-b)+6b=3(a-b)+6b=3a-3b+6b=3a+3b=3(a+b)=9， 故选C.

    查看答案和解析>>

    科目：初中数学 来源：江苏省2017-2018学年七年级12月月考数学试卷 题型：解答题

    阅读下表：

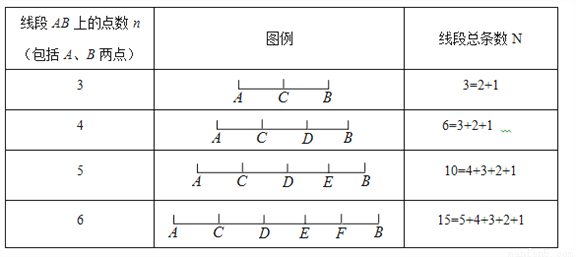
    解答下列问题：

    （1）猜测线段总条数N与线段上点数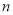（包括线段的两个端点）有什么关系；

    （2）当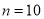时，求N的值．

    （1） ；（2）45． 【解析】试题分析：（1）(2)找规律可知是正整数前n项和. 试题解析：(1)根据规律可得数列规律是正整数的求和，利用（首项+末项）高可知，线段AB有第n点,1+2+3+4+……+n=. (2)由（1）公式有.

    查看答案和解析>>

    科目：初中数学 来源：江苏省2017-2018学年七年级12月月考数学试卷 题型：单选题

    一个正方体的每个面都写有一个汉字，其平面展开图如图所示，则在该正方体中，和“崇”相对的面上写的汉字是（　　）

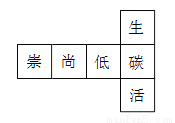
    A. 低 B. 碳 C. 生 D. 活

    A 【解析】空间想象或者亲手制作上图，可知选A.

    查看答案和解析>>

    科目：初中数学 来源：福建省2017-2018学年九年级数学上学期期末检测试卷 题型：解答题

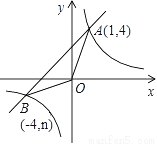
    如图，已知反比例函数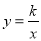的图象与一次函数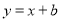的图象交于点A（1，4）、点B（－4，n）．

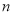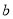    (1)求和的值；

    (2)求△OAB的面积；

    (3)直接写出一次函数值大于反比例函数值的自变量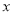的取值范围．

    （1）-1；（2）；（3）x＞1或﹣4＜x＜0. 【解析】试题分析：（1）把A的坐标代入反比例函数解析式求出A的坐标，把A的坐标代入一次函数解析式求出即可； （2）求出直线AB与y轴的交点C的坐标，分别求出△ACO和△BOC的面积，然后相加即可； （3）根据A、B的坐标结合图象即可得出答案． 试题解析： （1）把A点（1，4）分别代入反比例函数y=k/x，一次函数y=x+b，...

    查看答案和解析>>

    科目：初中数学 来源：福建省2017-2018学年九年级数学上学期期末检测试卷 题型：填空题

    在双曲线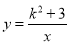上有三个点A（x1，y1），B（x2，y2），C（x3，y3），若x1＜x2＜0＜x3，则y1，y2 ，y3的大小关系是______________．（用“＜”连接）

    ． 【解析】试题解析： ∴双曲线在第三象限的图形单调递减， 故答案为：

    查看答案和解析>>

    科目：初中数学 来源：福建省2017-2018学年九年级数学上学期期末检测试卷 题型：单选题

    用配方法将方程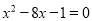变形为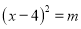的过程中，其中m的值正确的是（　　）

    A. 17 B. 15 C. 9 D. 7

    A 【解析】试题解析： 故选A.

    查看答案和解析>>

    科目：初中数学 来源：湖北省武汉市青山区2017-2018学年七年级（上）期中数学试卷 题型：填空题

    如图，第1个图是一个面积为a2的正方形，第2个图是由两个面积为a2的正方形构成，其中重叠部分面积为b2，第3个图是由三个面积为a2的正方形构成，其中重叠部分面积为2b2，如图依次叠放，则第11个图形的面积为_____．

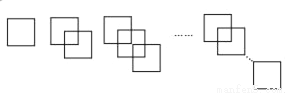
    11a2﹣10b2 【解析】试题解析：∵第1个图形的面积为a2， 第2个图形的面积为2a2﹣b2， 第3个图形的面积为3a2﹣2b2， … ∴第n个图形的面积为na2﹣（n﹣1）b2， ∴第11个图形的面积为11a2﹣10b2． 故答案为11a2﹣10b2．

    查看答案和解析>>

    科目：初中数学 来源：江苏省南通市2018届九年级上学期第三次月考数学试卷 题型：解答题

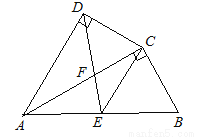
    如图四边形ABCD中，AC平分∠DAB，∠ADC=∠ACB=90°，E为AB的中点．

    (1) 求证：AC2=AB•AD；

    (2) 求证：CE∥AD；

    (3) 若AD=8，AB=12，求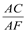的值．

    （1）证明见解析（2）证明见解析（3） 【解析】试题分析：（1）由AC平分∠DAB，∠ADC=∠ACB=90°，可证得△ADC∽△ACB，然后由相似三角形的对应边成比例，证得AC2=AB•AD； （2）由E为AB的中点，根据在直角三角形中，斜边上的中线等于斜边的一半，即可证得CE=AB=AE，继而可证得∠DAC=∠ECA，得到CE∥AD； （3）易证得△AFD∽△CFE，然后由相...

    查看答案和解析>>

    同步练习册答案