
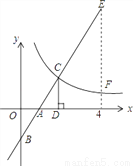
如图,在直角坐标系中,直线y1=2x﹣2与坐标轴交于A、B两点,与双曲线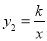 (x>0)交于点C,过点C作CD⊥x轴,且OA=AD,则以下结论: ①当x>0时,y1随x的增大而增大,y2随x的增大而减小;
(x>0)交于点C,过点C作CD⊥x轴,且OA=AD,则以下结论: ①当x>0时,y1随x的增大而增大,y2随x的增大而减小;
②k=4;
③当0<x<2时,y1<y2;
④如图,当x=4时,EF=4.
其中正确结论的个数是( )
A. 1 B. 2 C. 3 D. 4
C 【解析】对于直线y₁=2x?2, 令x=0,得到y=2;令y=0,得到x=1, ∴A(1,0),B(0,?2),即OA=1,OB=2, 在△OBA和△CDA中, , ∴△OBA≌△CDA(AAS), ∴CD=OB=2,OA=AD=1, ∴C(2,2), 当x>0时,y₁随x的增大而增大,y₂随x的增大而减小;故①正确; 把C坐标代入反比例解...科目:初中数学 来源:2017年海南省中考数学模拟试卷 题型:单选题
下列运算正确的是( )
A. 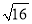 =8 B.
=8 B. 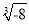 =﹣2 C.
=﹣2 C. 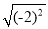 =﹣2 D.
=﹣2 D. 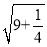 =3+
=3+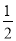
查看答案和解析>>
科目:初中数学 来源:2017年辽宁省营口市大石桥市水源镇中考数学模拟试卷(八) 题型:填空题
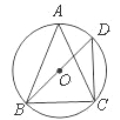
如图,⊙O是等腰三角形ABC的外接圆,AB=AC,∠A=45°,BD为⊙O的直径,BD= ,
,
连结CD,则BC= .
查看答案和解析>>
科目:初中数学 来源:2017年山东省临沂市中考数学二模试卷(一) 题型:解答题
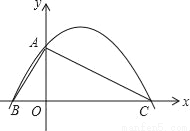
如图,在平面直角坐标系中,△ABC的边BC在x轴上,顶点A在y轴的正半轴上,OA=2,OB=1,OC=4.
(1)求过A、B、C三点的抛物线的解析式;
(2)设点M是x轴上的动点,试问:在平面直角坐标系中,是否存在点N,使得以点A,B,M,N为顶点的四边形是菱形?若存在,直接写出点N的坐标;若不存在,说明理由;
(3)若抛物线对称轴交x轴于点P,在平面直角坐标系中,是否存在点Q,使△PAQ是以PA为腰的等腰直角三角形?若存在,写出所有符合条件的点Q的坐标,选择一种情况加以说明;若不存在,说明理由.
查看答案和解析>>
科目:初中数学 来源:2017年山东省临沂市中考数学二模试卷(一) 题型:单选题
定义:给定关于x的函数y,对于该函数图象上任意两点(x1,y1),(x2,y2),当x1<x2时,都有y1<y2,称该函数为增函数,根据以上定义,可以判断下面所给的函数中,是增函数的有_____(填上所有正确答案的序号)
①y=2x;②y=﹣x+1;③y=x2(x>0);④y=﹣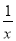 .
.
查看答案和解析>>
科目:初中数学 来源:2017年山东省临沂市中考数学二模试卷(一) 题型:单选题
把多项式4x2y﹣4xy2﹣x3分解因式的结果是( )
A. 4xy(x﹣y)﹣x3 B. ﹣x(x﹣2y)2
C. x(4xy﹣4y2﹣x2) D. ﹣x(﹣4xy+4y2+x2)
B 【解析】试题解析:4x2y-4xy2-x3 =-x(x2-4xy+4y2), =-x(x-2y)2. 故选B.查看答案和解析>>
科目:初中数学 来源:2017年山东省临沂市中考数学二模试卷(一) 题型:单选题
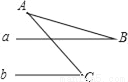
如图所示,直线a∥b,∠B=22°,∠C=50°,则∠A的度数为( )
A. 22° B. 28° C. 32° D. 38°
B 【解析】试题解析:如图, ∵a∥b, ∴∠1=∠C=50°, 又∠1=∠A+∠B, ∴∠A=∠1-∠B=50°-22°=28°, 故选B.查看答案和解析>>
科目:初中数学 来源:黄金30题系列 八年级数学 大题好拿分 题型:解答题
设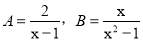 ,
,
(1) 求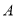 与
与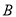 的差;
的差;
(2) 若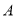 与
与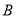 的值相等,求
的值相等,求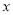 的值.
的值.
查看答案和解析>>
科目:初中数学 来源:湖南省衡阳市2017-2018学年八年级上期末模拟数学试卷(含答案) 题型:解答题
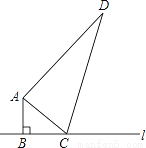
如图,在△ABC中,∠ABC=90°,AB=6cm,AD=24cm,BC与CD的长度之和为34cm,其中C是直线l上的一个动点,请你探究当C离点B有多远时,△ACD是以DC为斜边的直角三角形.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com