
 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案科目:初中数学 来源:浙江杭州下城区启正中学2017-2018学年八年级上学期中考试数学试卷(含解析) 题型:解答题
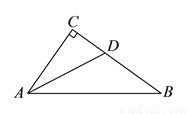
如图, 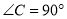 ,
, 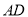 平分
平分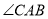 ,
, 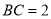 ,
, 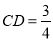 ,求
,求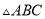 的面积.
的面积.
查看答案和解析>>
科目:初中数学 来源:浙江省金华市2017-2018学年八年级上册期末模拟数学试卷 题型:单选题
已知一个锐角三角形两边长分别为3,4,则第三边长不可能的值是( )
A、4 B、2 C、6 D、4.5
C 【解析】设第三边是x,由题意得: 4-3<x<4+3, 即:1<x<7. ∵三角形是锐角三角形, ∴a2+b2<c2, ∵A、4,在1<x<7范围内,a=3,b=4,c=4, ∴a2+b2>c2, 且故本选项A错误; B、2,在1<x<7范围内,a=2,b=3,c=4, ∴a2+b2<c2, 故本选项B错误; C、6,在1...查看答案和解析>>
科目:初中数学 来源:河南省禹州市2017-2018学年九年级上学期期中考试数学试卷 题型:单选题
已知一次函数y=a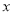 +b的图象经过第一、二、四象限,则在平面直角系数中二次函数y=a
+b的图象经过第一、二、四象限,则在平面直角系数中二次函数y=a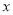 2+b
2+b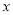 的图象大致是 ( )
的图象大致是 ( )
A. 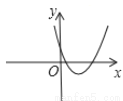 B.
B. 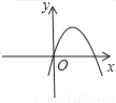 C.
C. 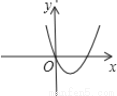 D.
D. 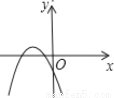
查看答案和解析>>
科目:初中数学 来源:河南省禹州市2017-2018学年九年级上学期期中考试数学试卷 题型:单选题
关于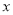 的一元二次方程
的一元二次方程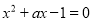 的根的情况是( )
的根的情况是( )
A. 有两个相等的实数根 B. 有两个不相等的实数根
C. 只有一个实数根 D. 没有实数根
B 【解析】△=a2?4×1×(?1)=a2+4. ∵a2?0, ∴a2+4>0,即△>0, ∴方程x2+ax?1=0有两个不相等的实数根. 故选:B.查看答案和解析>>
科目:初中数学 来源:2017年天津二十一中中考数学冲刺试卷(一) 题型:填空题
分解因式:x2﹣3x﹣4=_____;(a+1)(a﹣1)﹣(a+1)=_____.
(x﹣4)(x+1) (a+1)(a﹣2) 【解析】试题分析:根据分解因式的方法x2+(a+b)x+ab=(x+a)(x+b)和提公因式法进行分解即可. 【解析】 x2﹣3x﹣4=(x﹣4)(x+1), (a+1)(a﹣1)﹣(a+1)=(a+1)(a﹣1﹣1)=(a+1)(a﹣2), 故答案为:(x﹣4)(x+1),(a+1)(a﹣2).查看答案和解析>>
科目:初中数学 来源:2017年天津二十一中中考数学冲刺试卷(一) 题型:单选题
使两个直角三角形全等的条件是( )
A. 一锐角对应相等 B. 两锐角对应相等 C. 一条边对应相等 D. 两条边对应相等
D 【解析】试题分析:利用全等三角形的判定来确定.做题时,要结合已知条件与三角形全等的判定方法逐个验证. 【解析】 A、一个锐角对应相等,利用已知的直角相等,可得出另一组锐角相等,但不能证明两三角形全等,故A选项错误; B、两个锐角相等,那么也就是三个对应角相等,但不能证明两三角形全等,故B选项错误; C、一条边对应相等,再加一组直角相等,不能得出两三角形全等,故C选项错...查看答案和解析>>
科目:初中数学 来源:江苏省徐州市区联校2017-2018学年八年级上学期期中联考数学试卷 题型:填空题
等腰三角形的周长为13 cm,其中一边长是3 cm.则该等腰三角形的腰为____cm.
5 【解析】试题解析:当长是3cm的边是底边时,三边为3cm,5cm,5cm,等腰三角形成立; 当长是3cm的边是腰时,底边长是:13?3?3=7cm,而3+3<7,不满足三角形的三边关系. 故腰长是:5cm. 故答案为:5.查看答案和解析>>
科目:初中数学 来源:江苏省扬州市宝应县2018届九年级上学期12月月考数学试卷 题型:解答题
某商品的进价为每件50元,售价为每件60元,每天可卖出190件;如果每件商品的售价每上涨1元,则每天少卖10件,设每件商品的售价上涨x元(x为正整数),每天的销售利润为y元.
(1)求y关于x的关系式;
(2)每件商品的售价定为多少元时,每天的利润恰为1980元?
(3)每件商品的售价定为多少元时,每天可获得最大利润?最大利润是多少元?
(1)y=﹣10x2+90x+1900; (2)每件商品的售价定为61元或68元时,每天的利润恰为1980元; (3)每件商品的售价定为64元或65元时,每天可获得最大利润,最大利润是2100元. 【解析】试题分析:(1)利用销量乘以每件利润=总利润得出关系式即可; (2)利用(1)中所求关系式,进而使y=1980进而得出即可; (3)利用配方法求出二次函数最值,结合...查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com