
计算:
(1)(1.2×10-4)÷(2×10-2);
(2) 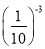 +
+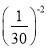 ×(π-4)0-(-3)3×0.3-1+|-27|.
×(π-4)0-(-3)3×0.3-1+|-27|.
 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源:北师大版数学七年级下册第一章整式乘法1.4整式的乘法课时练习 题型:单选题
(-x7)2·(x3y+z ) 等于( )
A. x17y+x14z B. -xy3+x3yz C. -x17y+x14z D. x17y+x3yz
A 【解析】【解析】 (-x7)2·(x3y+z )=x17y+x14z ,故选A.查看答案和解析>>
科目:初中数学 来源:北师大版数学七年级下册同步测试 1.5 平方差公式 题型:单选题
请你计算:
(1-x)(1+x),(1-x)(1+x+x2),…,
猜想(1-x)(1+x+x2+…+xn)的结果是( )
A. 1-xn+1 B. 1+xn+1 C. 1-xn D. 1+xn
A 【解析】已知各项利用平方差公式;多项式乘多项式法则计算,解题关键是要归纳总结得到一般性规律,即可得到答案. 【解析】 (1﹣x)(1+x)=1﹣x2, (1﹣x)(1+x+x2)=1+x+x2﹣x﹣x2﹣x3=1﹣x3, …, 依此类推(1﹣x)(1+x+x2+…+xn)=1﹣xn+1, 故选A.查看答案和解析>>
科目:初中数学 来源:北师大版七年级下册 第一章 整式的乘除 1.6完全平方公式 同步测试 题型:单选题
为了运用平方差公式计算(2x+y+z)(y-2x-z),下列变形正确的是( )
A. [2x-(y+z)]2
B. [2x+(y+z)][2x-(y+z)]
C. [y+(2x+z)][y-(2x+z)]
D. [z+(2x+y)][z-(2x+y)]
C 【解析】试题解析:根据题意分析:2x、z异号,y同号; ∴(2x+y+z)(y-2x-z)=[y+(2x+z)][y-(2x+z)]; 故选C.查看答案和解析>>
科目:初中数学 来源:北师大版七年级数学下1.3同底数幂的除法 第2课时 零指数幂与负整数指数幂 同步练习 题型:解答题
已知(2x-1)x+2=1,求整数x的值.
整数x的值是-2,0或1 【解析】试题分析:分当2x-1=1、2x-1=-1和2x-1≠0时三种情况求解即可. 试题解析: 分三种情况讨论:(1)因为1的任何次幂都是1,所以当2x-1=1时,解得x=1; (2)因为任何不等于零的数的零次幂都等于1,所以有2x-1≠0,且x+2=0,解得x=-2; (3)因为-1的偶次幂等于1,所以2x-1=-1,且x+2为偶数,解得...查看答案和解析>>
科目:初中数学 来源:北师大版七年级数学下1.3同底数幂的除法 第2课时 零指数幂与负整数指数幂 同步练习 题型:单选题
下列运算正确的是( )
A. a6÷a2=a3 B. (ab2)2=ab4 C. 2-3=-6 D. 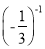 =-3
=-3
查看答案和解析>>
科目:初中数学 来源:北师大版七年级数学下1.3同底数幂的除法 第2课时 零指数幂与负整数指数幂 同步练习 题型:单选题
2﹣3可以表示为( )
A. 22÷25 B. 25÷22 C. 22×25 D. (﹣2)×(﹣2)×(﹣2)
A 【解析】根据负整数指数幂的运算法则可得;选项A,22÷25;选项B,25÷22;选项C,22×25;选项D,(﹣2)×(﹣2)×(﹣2)= .故选A.查看答案和解析>>
科目:初中数学 来源:2017-2018河北省保定市莲池区七年级第一学期数学期末试卷 题型:单选题
已知整数a0,a1,a2,a3,a4,……,满足下列条件: 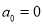 ,
, 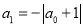 ,
, 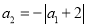 ,
, 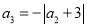 ,…,以此类推,则
,…,以此类推,则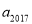 的值为( )
的值为( )
A. -1007 B. -1008 C. -1009 D. -2016
C 【解析】a0=0, =-|0+1|=-1, =-|-1+2|=-1, =-|-1+3|=-2, a4=-|a3+4|=-|-2+4|=-2, …, 所以,n是偶数时,an=-;n是奇数时,an=- , a2017=- . 故选C.查看答案和解析>>
科目:初中数学 来源:北师大版八年级下册数学 第二章 一元一次不等式与一元一次不等式组 单元检测卷 题型:填空题
若关于x的不等式3m+x>5的解集是x>2,则m的值是________
1 【解析】首先求出不等式的解集,然后与x>2比较,就可以得出m的值. 【解析】 解不等式3m-2x<5, 得x>, 又∵此不等式的解集是x>2, ∴=2, ∴m=3. 主要考查了一元一次不等式的解法.解一元一次不等式的一般步骤是:去分母,去括号,移项,合并同类项,系数化为1.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com