
计算(﹣2)2015+(﹣2)2016等于( )
A. ﹣24031 B. ﹣22015 C. 22014 D. 22015
D 【解析】根据乘方的意义,可知:(﹣2)2015+(﹣2)2016, =(﹣2)2015+(﹣2)×(﹣2)2015, =(1﹣2)×(﹣2)2015, =(﹣1)×(﹣2)2015, =22015. 故选:D.科目:初中数学 来源:2017年湖北省黄冈市中考数学三模试卷 题型:填空题
抛物线y=2x2+6x+c与x轴的一个交点为(1,0),则这个抛物线的顶点坐标是_____.
(-,- ) 【解析】试题解析:∵抛物线y=2x2+6x+c与x轴的一个交点为(1,0) 即抛物线经过点(1,0) 代入解析式得到c=-8 ∴解析式是y=2x2+6x-8 ∵y=ax2+bx+c的顶点坐标公式为(?, ) 代入公式求值得到顶点坐标是(?,?) 故填(-,?).查看答案和解析>>
科目:初中数学 来源:2017广东省深圳市中考数学模拟试卷(三) 题型:单选题
﹣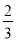 的倒数是( )
的倒数是( )
A. 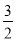 B. ﹣
B. ﹣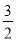 C.
C. 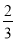 D. ﹣
D. ﹣
查看答案和解析>>
科目:初中数学 来源:2016-2017学年陕西省七年级(下)第二次测验数学试卷 题型:填空题
方程(a-2)x|a|-1+3=0是关于x的一元一次方程,则a=____.
-2 【解析】试题解析:根据一元一次方程的定义,可得: 解得: 把代入方程得: 解得: 故答案为:查看答案和解析>>
科目:初中数学 来源:2016-2017学年陕西省七年级(下)第二次测验数学试卷 题型:单选题
某学校七年级(3)班共有50名学生,老师对学生最喜欢的一种球类运动进行了调查,并根据调查的结果制作了如图扇形统计图(不完整),请你根据扇形统计图中提供的信息判断下列说法错误的是( )
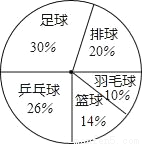
A. 最喜欢足球的人数最多,达到了15人
B. 最喜欢羽毛球的人数比例最少,只有10%
C. 图中表示排球的扇形的圆心角为50°
D. 最喜欢乒乓球的人数比最喜欢篮球的人数多6人
C 【解析】根据扇形统计图,分析数据可得: A、∵七年级(3)班共有50名学生,最喜欢足球的人数占到30%, ∴最喜欢足球的人数最多,达到了:50×30%=15(人),此选项正确不合题意; B、利用扇形统计图可得出:最喜欢羽毛球的人数比例最少,只有10%,此选项正确不合题意; C、图中表示排球的扇形的圆心角为:360°×20%=72°,故此选项错误符合题意; D...查看答案和解析>>
科目:初中数学 来源:江苏省徐州市丰县2017-2018学年八年级上学期第二次月考数学试卷 题型:解答题
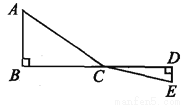
如图,C为线段BD上一动点,分别过点B、D作AB⊥BD,ED⊥BD,连接AC、EC.已知AB=5,DE=1,BD=8,设CD=x.
(1)用含x的代数式表示AC+CE的长.
(2)请问点C满足什么条件时,AC+CE的值最小?并求出最小值;
(3)根据(2)中的规律和结论,请构图求出代数式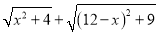 的最小值.
的最小值.
查看答案和解析>>
科目:初中数学 来源:江苏省徐州市丰县2017-2018学年八年级上学期第二次月考数学试卷 题型:填空题
已知一个直角三角形的两边长分别为3和4,则第三边长是__________
5或 【解析】试题分析:分两种情况(1)3和4都是直角边,由勾股定理求得斜边为5;(2)3是直角边,4是斜边,由勾股定理求得另一条直角边为.查看答案和解析>>
科目:初中数学 来源:安徽省16-17学年度第一学期七年级数学期末考试卷 题型:填空题
某种钢笔标价为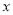 元,若购买20支及以上有8折优惠,甲买20支这种笔比乙买8支多用40元,则
元,若购买20支及以上有8折优惠,甲买20支这种笔比乙买8支多用40元,则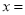 ________.
________.
查看答案和解析>>
科目:初中数学 来源:黑龙江省哈尔滨市香坊区2017年中考数学二模试卷(解析版) 题型:解答题
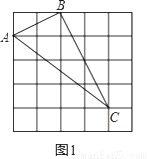
图1,图2是两张形状和大小完全相同的方格纸,方格纸中每个小正方形的边长均为1,线段AB的两个端点均在小正方形的顶点上.
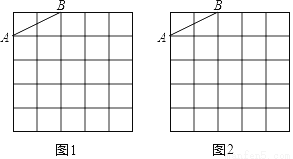
(1)如图1,在小正方形的顶点上确定一点C,连接AC、BC,使得△ABC为直角三角形,其面积为5,并直接写出△ABC的周长;
(2)如图2,在小正方形的顶点上确定一点D,连接AD、BD,使得△ABD中有一个内角为45°,且面积为3.
【答案】(1)5+3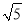 ;(2)3.
;(2)3.
【解析】试题分析:(1)构造直角三角形,AB=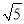 且是直角边,面积是5,可以求出另外一条直角边BC长度,最后连接AC.
且是直角边,面积是5,可以求出另外一条直角边BC长度,最后连接AC.
(2)先构造一个45°角,再利用面积是3,可画出图象.
试题解析:
(1)【解析】
如图1所示:△ABC即为所求,
△ABC的周长为: 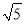 +2
+2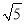 +5=5+3
+5=5+3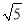 ;
;
(2)【解析】
如图2所示:△ABD中,∠ADB=45°,且面积为3.
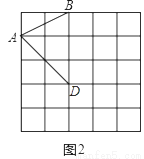
【题型】解答题
【结束】
23
为了解青少年形体情况,现随机抽查了若干名初中学生坐姿、站姿、走姿的好坏情况(如果一个学生有一种以上不良姿势,以他最突出的一种作记载),并将统计结果绘制了如下两幅不完整的统计图,请根据图中所给信息解答下列问题:
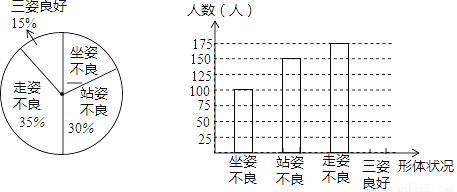
(1)求这次被抽查形体测评的学生一共有多少人?
(2)求在被调查的学生中三姿良好的学生人数,并将条形统计图补充完整;
(3)若全市有5万名初中生,那么估计全市初中生中,坐姿和站姿不良的学生共有多少人?
(1)500名;(2)75名;(3)2.5万 【解析】试题分析:(1)用类型人数除以所占百分比就是总人数.(2)用总人数乘以15%. (3) 坐姿和站姿不良的学生的学生的百分比乘以总人数. 试题解析: (1)【解析】 100÷20%=500(名), 答:这次被抽查形体测评的学生一共是500名; (2)【解析】 三姿良好的学生人数:500×15%=75名, ...查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com