
老师在黑板上写了一个正确的演算过程,随后用手掌捂住了多项式,形式如下
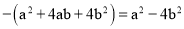
(1)求所捂的多项式;
(2)当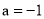 ,
, 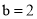 时,求所捂的多项式的值.
时,求所捂的多项式的值.
 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源:北师大版数学九年级上册第二章第三节《用公式法求解一元一次方程》课时练习 题型:单选题
已知4个数据:?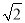 ,2
,2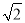 ,a,b,其中a、b是方程
,a,b,其中a、b是方程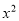 -2x-1=0的两个根,则这4个数据的中位数是( )
-2x-1=0的两个根,则这4个数据的中位数是( )
A. 1 B. 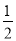 C. 2 D.
C. 2 D. 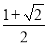
查看答案和解析>>
科目:初中数学 来源:北师大版九年级数学(上)第二章《一元二次方程》同步测试:2.4用因式分解法求解一元二次方程 题型:单选题
现定义运算“★”,对于任意实数a、b,都有a★b= 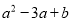 ,如:3★5=
,如:3★5=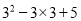 ,若x★2=6,则实数x的值是( )
,若x★2=6,则实数x的值是( )
A. 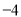 或
或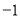 B. 4或
B. 4或 C. 4或
C. 4或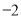 D.
D. 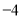 或2
或2
查看答案和解析>>
科目:初中数学 来源:初三数学第一学期1.1.1菱形的定义与性质 同步练习 题型:填空题
四边形ABCD是菱形,∠BAD=60°,AB=6,对角线AC与BD相交于点O,点E在AC上,若OE=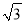 ,则CE的长为______.
,则CE的长为______.
查看答案和解析>>
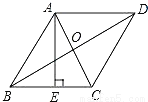
科目:初中数学 来源:初三数学第一学期1.1.1菱形的定义与性质 同步练习 题型:单选题
如图,菱形ABCD的对角线AC、BD的长分别是6cm、8cm,AE⊥BC于点E,则AE的长是( )
A. 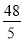 cm B.
cm B. 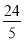 cm C.
cm C. 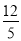 cm D.
cm D. 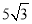 cm
cm
查看答案和解析>>
科目:初中数学 来源:广西柳州市2017-2018学年七年级上学期期末考试数学试卷 题型:填空题
某商店换季促销,将一件标价为240元的T恤8折售出,仍获利20%,若设这件T恤的成本是x元,根据题意,可得到的方程是____.
240×0.8-x=20%x 【解析】【解析】 设这件T恤的成本是x元,根据标价为240元的T恤8折售出,仍获利20%,得: 240×0.8-x=20%x.故答案为:240×0.8-x=20%x.查看答案和解析>>
科目:初中数学 来源:广西柳州市2017-2018学年七年级上学期期末考试数学试卷 题型:单选题
在灯塔O处观测到轮船A位于北偏西54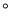 的方向,同时轮船B在南偏东15
的方向,同时轮船B在南偏东15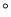 的方向,则∠AOB的大小为( )
的方向,则∠AOB的大小为( )
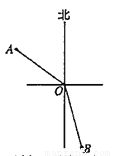
A. 69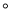 B. 111
B. 111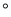 C. 159
C. 159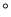 D. 141
D. 141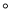
查看答案和解析>>
科目:初中数学 来源:广东省广州市天河区2017-2018学年七年级上学期期末考试数学试卷 题型:填空题
如图,把一张长方形纸片沿AB折叠后,若∠1=50°,则∠2的度数为______.
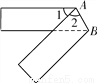
查看答案和解析>>
科目:初中数学 来源:甘肃省天水市2018届九年级上学期期末模四考试数学试卷 题型:单选题
△ABC与△A′B′C′是位似图形,且△ABC与△A′B′C′的位似比是1:2,已知△ABC的面积是3,则△A′B′C′的面积是( )
A. 3 B. 6 C. 9 D. 12
D 【解析】试题分析:根据位似比可得:△ABC的面积:△A′B′C′的面积=1:4,则△A′B′C′的面积=12.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com