练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    下列方程是一元一次方程的是（　　）

    A. x+2y=9 B. x2－3x=1 C. 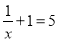D. x+1=1

    D 【解析】A. x+2y=9，含有两个未知数，不符合题意；B. x2－3x=1，最高次是2次，不符合题意；C. ，不是整式方程，不符合题意； D. x+1=1，是一元一次方程，符合题意， 故选D.
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源：江西省萍乡市2017-2018学年七年级上学期期末考试数学试卷 题型：填空题

    用同样大小的黑色棋子按如图所示的规律摆放：

    则第5个图案有____个棋子，第n个图案有____个棋子．（用含n的式子表示）

    18 3n+3． 【解析】试题解析：∵第1个图形有6个棋子， 第2个图形有6+3=9个棋子， 第3个图形有6+3×2=12个棋子， 第4个图形有6+3×4=18个棋子， ∴第5个图形有18个棋子， ∴第n个图形有棋子(3n+3)个[或6+3(n?1)等]. 故答案为：18，3n+3.

    查看答案和解析>>

    科目：初中数学 来源：江苏省泰兴市2018届九年级上学期期末考试数学试卷 题型：单选题

    已知x=2是一元二次方程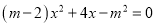的一个根，则m的值为 （ ）

    A. 2 B. 0或2 C. 0或4 D. 0

    C 【解析】把x=2代入得， ， 解之得 m=0或m=4. 故选C.

    查看答案和解析>>

    科目：初中数学 来源：甘肃省天水市2017-2018学年七年级上学期期末模四考试数学试卷 题型：填空题

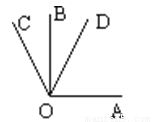
    如图，OA⊥OB，∠BOC=300，OD平分∠AOC，则∠BOD= _____．

    30° 【解析】∵OA⊥OB，∴∠AOB=90°， ∵∠BOC=30°，∴∠AOC=∠AOB+∠BOC=120°， ∵OD平分∠AOC，∴∠AOD=∠AOC=60°， ∴∠BOD=∠AOB-∠AOD=30°， 故答案为：30°.

    查看答案和解析>>

    科目：初中数学 来源：甘肃省天水市2017-2018学年七年级上学期期末模四考试数学试卷 题型：单选题

    已知代数式x＋2y的值是3，则代数式2x＋4y＋1的值是（　　）

    A. 1 B. 7 C. 4 D. 不能确定

    B 【解析】∵x+2y=3， ∴2x+4y+1=2(x+2y)+1=2×3+1=7， 故选B.

    查看答案和解析>>

    科目：初中数学 来源：江苏省扬州市邗江区2018届九年级上学期期末考试数学试卷 题型：解答题

    如图，BE是⊙O的直径，点A在EB的延长线上，弦PD⊥BE，垂足为C，连接OD，∠AOD＝∠APC.

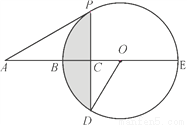
    (1)求证：AP是⊙O的切线；

    (2)若⊙O的半径是4，AP＝4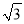，求图中阴影部分的面积．

    (1)证明见解析;(2) =. 【解析】试题分析：（1）连接OP，要证AP是⊙O的切线，只需 根据条件证得∠APO=90°即可；（2）分别求出△DPO和扇形OPBD的面积，然后利用S阴影=S扇形OPBD－S△OPD计算即可． 试题解析：【解析】 （1）证明：连接OP，则OD=OP， ∴∠OPD=∠ODP， ∴∠APC=∠AOD， ∴∠OPD+∠APC=∠ODP+∠A...

    查看答案和解析>>

    科目：初中数学 来源：江苏省扬州市邗江区2018届九年级上学期期末考试数学试卷 题型：填空题

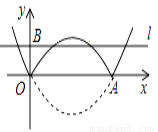
    在平面直角坐标系中，抛物线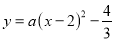经过原点O，与x轴的另一个交点为A．将抛物线在x轴下方的部分沿x轴折叠到x轴上方，将这部分图象与原抛物线剩余部分的图象组成的新图象记为G，过点B（0，1）作直线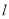平行于x轴，当图象G在直线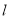上方的部分对应的函数y随x增大而增大时，x的取值范围是___．

    或 【解析】试题解析： ∵抛物线经过原点 图象G对应的函数解析式为： ， 如图③，由题意得： 当时， 解得： 当时， 解得： 由图象得：图象在直线上方的部分，当或时，函数随增大而增大； 故答案为： 或.

    查看答案和解析>>

    科目：初中数学 来源：北京市延庆区2017-2018学年第一学期八年级期末数学试卷 题型：解答题

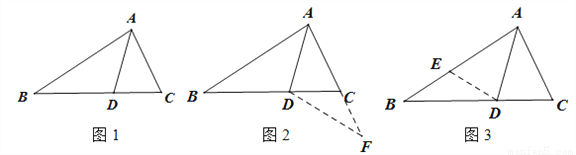
    如图1，△ABC中，AD是∠BAC的平分线，若AB=AC+CD，那么∠ACB与∠ABC有怎样的数量关系呢？

    （1）通过观察、实验提出猜想：∠ACB与∠ABC的数量关系，用等式表示为： ．

    （2）小明把这个猜想与同学们进行交流，通过讨论，形成了证明该猜想的几种想法：

    想法1：如图2，延长AC到F，使CF=CD，连接DF．通过三角形全等、三角形的性质等知识进行推理，就可以得到∠ACB与∠ABC的数量关系．

    想法2：在AB上取一点E，使AE=AC，连接ED，通过三角形全等、三角形的性质等知识进行推理，就可以得到∠ACB与∠ABC的数量关系．

    请你参考上面的想法，帮助小明证明猜想中∠ACB与∠ABC的数量关系（一种方法即可）．

    （1）∠ACB=2∠ABC；（2）答案见解析 【解析】（1）根据已知条件并通过观察、比较、测量、证明等方法即可猜想出结论； （2）根据全等三角形的性质和等腰三角形的性质及三角形的外角即可得到结论． 【解析】 （1）∠ACB=2∠ABC （2）想法1： ∵ AD是∠BAC的平分线， ∴∠BAD=∠CAD， ∵AF=AC+CF，且CD=CF， ∴AF=...

    查看答案和解析>>

    科目：初中数学 来源：2017-2018学年度第一学期海口市八年级数学科期末检测模拟题（实验班卷） 题型：单选题

    如图，在□ABCD中，AB=4，AD=7，∠ABC平分线交AD于点E，交CD的延长线于点F，则DF的长是（ ）

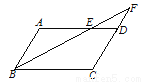
    A. 2 B. 3 C. 4 D. 5

    B 【解析】试题分析：∵平行四边形ABCD ∴AB∥CD ∴∠ABE=∠CFE ∵∠ABC的平分线交AD于点E ∴∠ABE=∠CBF ∴∠CBF=∠CFB ∴CF=CB=7 ∴DF=CF-CD=7-4=3 故选D．

    查看答案和解析>>

    同步练习册答案