
下列各数中,与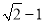 的积为有理数的是( )
的积为有理数的是( )
A. 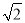 B.
B. 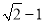 C.
C.  D.
D. 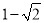
科目:初中数学 来源:北京市分校2017-2018学年度第一学期八年级数学期中试卷 题型:解答题
如图,在四边形 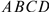 中,
中, ,
, .请你添加一条线把它分成两个全等三角形,并给出证明.
.请你添加一条线把它分成两个全等三角形,并给出证明.
查看答案和解析>>
科目:初中数学 来源:2017-2018学年八年级数学下册(人教版):期中检测题 题型:单选题
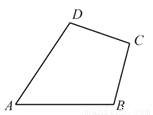
如图,任意四边形ABCD中,E,F,G,H分别是AB,BC,CD,DA上的点,对于四边形EFGH的形状,某班学生在一次数学活动课中,通过动手实践,探索出如下结论,其中错误的是( )
A.当E,F,G,H是各边中点,且AC=BD时,四边形EFGH为菱形
B.当E,F,G,H是各边中点,且AC⊥BD时,四边形EFGH为矩形
C.当E,F,G,H不是各边中点时,四边形EFGH可以为平行四边形
D.当E,F,G,H不是各边中点时,四边形EFGH不可能为菱形
D 【解析】 试题分析: 根据题意,可知,连接四边形各边中点所得的四边形必为平行四边形,根据中点四边形的性质进行判断: A.当E,F,G,H是各边中点,且AC=BD时,EF=FG=GH=HE,故四边形EFGH为菱形,故A正确; B.当E,F,G,H是各边中点,且AC⊥BD时,∠EFG=∠FGH=∠GHE=90°,故四边形EFGH为矩形,故B正确; C.当E,F,...查看答案和解析>>
科目:初中数学 来源:2017-2018学年度第一学期海南省九年级数学科期末检测模拟试卷 题型:填空题
如图,在梯形ABCD中,AD∥BC,E和F分别是AB和CD的中点,连结EF,若EF=7,则AD+BC=_______.

查看答案和解析>>
科目:初中数学 来源:2017-2018学年度第一学期海南省九年级数学科期末检测模拟试卷 题型:单选题
如图,修建抽水站时,沿着坡度为i=1:6的斜坡铺设管道. 下列等式成立的是( )

A. sinα =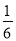 B. cosα=
B. cosα=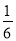 C. tanα=
C. tanα=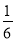 D. cotα=
D. cotα=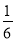
查看答案和解析>>
科目:初中数学 来源:2017-2018学年山东省济宁市嘉祥县九年级(上)月考数学试卷 题型:解答题
如图,已知AB是⊙O的直径,点C、D在⊙O上,点E在⊙O外,∠EAC=∠D=60°.
(1)求∠ABC的度数;
(2)求证:AE是⊙O的切线;
(3)当BC=4时,求劣弧AC的长.

查看答案和解析>>
科目:初中数学 来源:2017-2018学年山东省济宁市嘉祥县九年级(上)月考数学试卷 题型:填空题
如图,PA、PB是⊙O的切线,A、B为切点,AC是⊙O的直径,∠P=50°,则∠BAC=______.
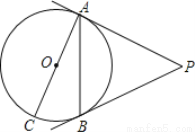
查看答案和解析>>
科目:初中数学 来源:山东省淄博市2018届九年级上学期期中考试数学试卷 题型:解答题
计算(1)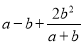
(2)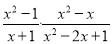
查看答案和解析>>
科目:初中数学 来源:上海市崇明区2018届九年级上学期期末调研测试数学试卷 题型:单选题
如图,在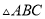 中,点D,E分别在边AB,AC上,
中,点D,E分别在边AB,AC上, 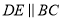 .已知
.已知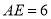 ,
, 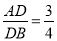 ,
,
那么EC的长是( )
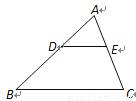
A. 4.5 B. 8 C. 10.5 D. 14
B 【解析】试题解析:∵DE∥BC. ∴, 而AE=6, , ∴, ∴EC=8, 故选B.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com