
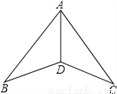
如图,在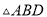 和
和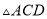 中,已知
中,已知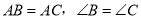 ,求证:AD是
,求证:AD是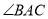 的平分线.
的平分线.
 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源:湖南省2018届九年级上学期期末考试数学试卷 题型:单选题
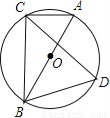
如图,⊙O的直径AB=2,弦AC=1,点D在⊙O上,则∠D的度数是( )
A. 30° B. 45° C. 60° D. 75°
C 【解析】试题分析:由⊙O的直径是AB,得到∠ACB=90°,根据特殊三角函数值可以求得∠B的值,继而求得∠A和∠D的值. 【解析】 ∵⊙O的直径是AB, ∴∠ACB=90°, 又∵AB=2,弦AC=1, ∴sin∠CBA=, ∴∠CBA=30°, ∴∠A=∠D=60°, 故选:C.查看答案和解析>>
科目:初中数学 来源:江苏省兴化市顾庄学区2017-2018学年八年级上学期期末考试数学试卷 题型:解答题
如图,在平行四边形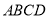 中,∠BAD的平分线交
中,∠BAD的平分线交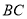 于E,点
于E,点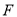 在
在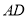 上,且
上,且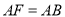 ,连接
,连接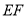 .
.
(1) 判断四边形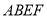 的形状并证明;
的形状并证明;
(2) 若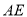 、
、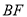 相交于点
相交于点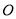 ,且四边形
,且四边形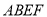 的周长为
的周长为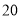 ,
, 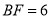 ,求
,求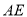 的长度及四边形
的长度及四边形 的面积.
的面积.
查看答案和解析>>
科目:初中数学 来源:江苏省兴化市顾庄学区2017-2018学年八年级上学期期末考试数学试卷 题型:单选题
已知直线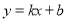 不经过第三象限,则下列结论正确的是( )
不经过第三象限,则下列结论正确的是( )
A.k>0, b>0; B.k<0, b>0; C.k<0, b<0; D.k<0, b≥0
D. 【解析】 试题分析:∵直线不经过第三象限,∴k<0,b≥0.故选D.查看答案和解析>>
科目:初中数学 来源:云南民族大学附属中学2017-2018学年八年级上学期期末考试数学试卷 题型:解答题
甲从一个鱼摊上买了三条鱼,平均每条a元,又从另一个鱼摊上买了两条鱼,平均每条b元,后来他又以每条 元的价格把鱼全部卖给了乙,请问甲会赚钱还是赔钱?并说明原因.
元的价格把鱼全部卖给了乙,请问甲会赚钱还是赔钱?并说明原因.
查看答案和解析>>
科目:初中数学 来源:云南民族大学附属中学2017-2018学年八年级上学期期末考试数学试卷 题型:填空题
若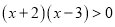 ,则x的取值范围是______ .
,则x的取值范围是______ .
查看答案和解析>>
科目:初中数学 来源:云南民族大学附属中学2017-2018学年八年级上学期期末考试数学试卷 题型:单选题
面积相等的两个三角形
A. 必定全等 B. 必定不全等
C. 不一定全等 D. 以上答案都不对
C 【解析】【解析】 面积相等的两个三角形不一定全等.故选C.查看答案和解析>>
科目:初中数学 来源:贵州省遵义市桐梓县2016-2017学年七年级上学期期末考试数学试卷 题型:填空题
若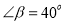 ,则
,则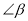 的补角等于________.
的补角等于________.
查看答案和解析>>
科目:初中数学 来源:云南省双柏县2017-2018学年八年级上期期末数学试卷 题型:解答题
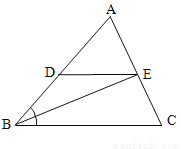
如图,已知DE∥BC,BE是∠ABC的平分线,∠C=70°,∠ABC=50°.求∠DEB和∠BEC的度数.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com