
 课堂全解字词句段篇章系列答案
课堂全解字词句段篇章系列答案 步步高口算题卡系列答案
步步高口算题卡系列答案 点睛新教材全能解读系列答案
点睛新教材全能解读系列答案科目:初中数学 来源:河南省2017-2018学年八年级上学期期末考试数学试卷 题型:单选题
下列计算正确的是( )
A. 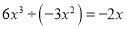 B.
B. 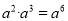 C.
C. 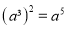 D.
D. 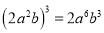
查看答案和解析>>
科目:初中数学 来源:北京市密云区2017-2018学年度第一学期期末考试初三数学试卷 题型:填空题
抛物线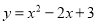 的对称轴方程是____________________.
的对称轴方程是____________________.
查看答案和解析>>
科目:初中数学 来源:北京大兴区2017-2018学年度第一学期期末检测试卷 题型:解答题
在一次社会大课堂的数学实践活动中,王老师要求同学们测量教室窗户边框上的点C到地面的距离即CD的长,小英测量的步骤及测量的数据如下:
(1)在地面上选定点A, B,使点A,B,D在同一条直线上,测量出 、
、 两点间的距离为9米;
两点间的距离为9米;
(2)在教室窗户边框上的点C点处,分别测得点 ,
, 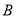 的俯角∠ECA=35°,∠ECB=45°.请你根据以上数据计算出
的俯角∠ECA=35°,∠ECB=45°.请你根据以上数据计算出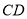 的长.
的长.
(可能用到的参考数据:sin35°≈0.57 cos35°≈0.82 tan35°≈0.70)

查看答案和解析>>
科目:初中数学 来源:北京大兴区2017-2018学年度第一学期期末检测试卷 题型:填空题
若函数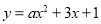 的图象与
的图象与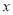 轴有两个交点,则
轴有两个交点,则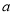 的取值范围是____________.
的取值范围是____________.
查看答案和解析>>
科目:初中数学 来源:北京大兴区2017-2018学年度第一学期期末检测试卷 题型:单选题
将抛物线y=5x2先向右平移2个单位,再向下平移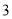 个单位,可以得到新的抛物线是
个单位,可以得到新的抛物线是
A. y=5(x+2)2+3 B. y=5(x-2)2+3 C. y=5(x+2)2-3 D. y=5(x-2)2-3
D 【解析】将抛物线y=5x2先向右平移2个单位得y=5(x-2)2,再向下平移个单位得y=5(x-2)2-3. 故选D.查看答案和解析>>
科目:初中数学 来源:湖南省娄底市娄星区2017-2018学年七年级上学期期末考试数学试卷 题型:解答题
某生物课外活动小组的同学举行植物标本制作比赛,结果统计如下:

根据表中提供的信息,回答下列问题:
(1)该组共有学生多少人?
(2)每人制作标本数在6个及以上的人数在全组人数中所占比例?
(3)平均每人制作多少个标本?
(4)补全下图的条形统计图.
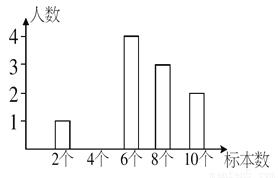
查看答案和解析>>
科目:初中数学 来源:湖南省娄底市娄星区2017-2018学年七年级上学期期末考试数学试卷 题型:单选题
若点C在线段AB上,不能判断点C是线段AB的中点的式子是( )
A. AB=2AC B. BC=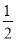 AB C. AC=BC D. AC+BC=AB
AB C. AC=BC D. AC+BC=AB
查看答案和解析>>
科目:初中数学 来源:北京市东城区2017--2018学年第一学期期末练习初一数学试卷 题型:填空题
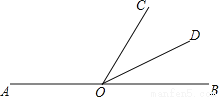
如图,点A、O、B在一条直线上,∠AOC=140°,OD是∠BOC的平分线,则∠COD= 度.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com