
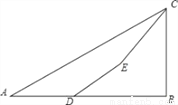
如图,为了测量某建筑物BC的高度,小明先在地面上用测角仪自A处测得建筑物顶部的仰角是30°,然后在水平地而上向建筑物前进了50m到达D处,此时遇到一斜坡,坡度i=1: 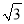 ,沿着斜坡前进20米到达E处测得建筑物顶部的仰角是45°,(坡度i=1:
,沿着斜坡前进20米到达E处测得建筑物顶部的仰角是45°,(坡度i=1: 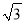 是指坡面的铅直高度FE与水平宽度DE的比).请你计算出该建筑物BC的高度.(取
是指坡面的铅直高度FE与水平宽度DE的比).请你计算出该建筑物BC的高度.(取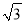 =1.732,结果精确到0.1m).
=1.732,结果精确到0.1m).
科目:初中数学 来源:浙江省金华市2017-2018学年七年级上册期末模拟数学试卷 题型:单选题
某商店有两个进价不同的计算器都卖了64元,其中一个盈利60%,另一个亏本20%,在这项买卖中,这家商店( )
A.赔了8元 B.赚了32元 C.不赔不赚 D.赚了8元
D 【解析】本题考查的是一元一次方程的应用 要计算赔赚,就要分别求出两个计算器的进价,再与售价作比较即可.因此就要先设出未知数,根据进价+利润=售价,利用题中的等量关系列方程求解. 设盈利60%的进价为x元, 则:x+60%x=64, 解得:x=40, 再设亏损20%的进价为y元,则; y-20%y=64, 解得:y=80, 所以总进价是120元,总售价是128元,售...查看答案和解析>>
科目:初中数学 来源:重庆市长寿区2017-2018学年七年级(上)期中数学 题型:解答题
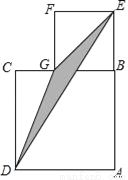
如图,正方形ABCD与正方形BEFG,且A,B,E在一直线上,已知AB=a,BE=b(b<a).
(1)用a、b的代数式表示△ADE的面积.
(2)用a、b的代数式表示△DCG的面积.
(3)用a、b的代数式表示阴影部分的面积.
查看答案和解析>>
科目:初中数学 来源:重庆市长寿区2017-2018学年七年级(上)期中数学 题型:单选题
下列多项式中,与﹣x﹣y相乘的结果是x2﹣y2的多项式是( )
A. y﹣x B. x﹣y C. x+y D. ﹣x﹣y
A 【解析】∵, ∴与相乘的结果是的是. 故选A.查看答案和解析>>
科目:初中数学 来源:浙江省宁波市2018届九年级上册期末模拟数学试卷 题型:解答题
已知二次函数y=x2﹣2x﹣3与x轴交于A、B两点(A在B的左边),与y轴交于点C.
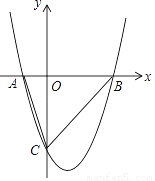
(1)求出点A、B、C的坐标.
(2)求S△ABC
(3)在抛物线上(除点C外),是否存在点N,使得S△NAB=S△ABC , 若存在,求出点N的坐标,若不 存在,请说明理由.
(1)A(﹣1,0)、B(3,0);(2)6;(3)存在,点N的坐标(1+ ,3)或(1﹣,3)或(2,﹣3) 【解析】试题分析: (1)在解析式中,由,求得的对应值可得点C的坐标;由,求得对应的的值可得点A、B的坐标; (2)根据(1)中所求点A、B、C坐标可求得△ABC的面积; (3)设点N的纵坐标为,则由S△NAB=S△ABC可知或,由点N在抛物线上,可得或,解方程即...查看答案和解析>>
科目:初中数学 来源:浙江省宁波市2018届九年级上册期末模拟数学试卷 题型:填空题
计算:cos30°﹣sin60°=________.
0. 【解析】原式=? =0, 故答案为:0.查看答案和解析>>
科目:初中数学 来源:浙江省宁波市2018届九年级上册期末模拟数学试卷 题型:单选题
在Rt△ABC中,∠C=90°,若斜边上的高为h,sinA= , 则AB的长等于( )
, 则AB的长等于( )
A. 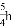 B.
B. 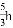 C.
C. 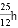 D.
D. 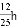
查看答案和解析>>
科目:初中数学 来源:2017年河北省沧州市中考数学模拟试卷(六) 题型:解答题
计算:(﹣1)﹣2+2sin245°﹣(1﹣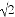 )0
)0
查看答案和解析>>
科目:初中数学 来源:山东省2017-2018学年七年级12月月考数学试卷 题型:解答题
列方程解应用题:
甲骑摩托车,乙骑自行车同时从相距150千米的两地相向而行,经过5小时相遇,已知甲每小时行驶的路程是乙每小时行驶的路程的3倍少6千米,求乙骑自行车的速度.
乙骑自行车的速度为9千米/时. 【解析】试题分析:本题考查了一元一次方程的应用---行程问题,设乙骑自行车的速度为x千米/时,则甲的速度为(3x-6)千米/时,根据相遇问题的数量关系建立方程求出其解即可. 【解析】 设乙骑自行车的速度为x千米/时, 据题意得 5(3x-6)+5x =150. 解得x=9. 答:乙骑自行车的速度为9千米/时.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com