
如图,在Rt△ABC中,∠ACB=90°,AO是△ABC的角平分线.以O为圆心,OC为半径作⊙O.
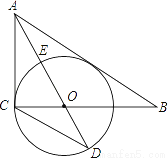
(1)求证:AB是⊙O的切线.
(2)已知AO交⊙O于点E,延长AO交⊙O于点D,tanD=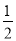 ,求
,求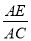 的值.
的值.
(3)在(2)的条件下,设⊙O的半径为3,求AB的长.
【答案】(1)证明见解析(2)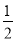 (3)
(3)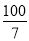
【解析】试题分析:(1)过O作OF⊥AB于F,由角平分线上的点到角两边的距离相等即可得证;(2)连接CE,证明△ACE∽△ADC可得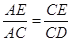 = tanD=
= tanD=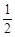 ;(3)先由勾股定理求得AE的长,再证明△B0F∽△BAC,得
;(3)先由勾股定理求得AE的长,再证明△B0F∽△BAC,得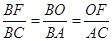 ,设BO="y" ,BF=z,列二元一次方程组即可解决问题.
,设BO="y" ,BF=z,列二元一次方程组即可解决问题.
试题解析:(1)证明:作OF⊥AB于F
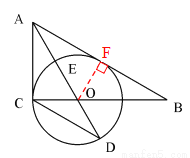
∵AO是∠BAC的角平分线,∠ACB=90º
∴OC=OF
∴AB是⊙O的切线
(2)连接CE
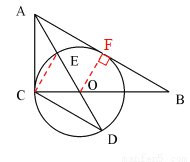
∵AO是∠BAC的角平分线,
∴∠CAE=∠CAD
∵∠ACE所对的弧与∠CDE所对的弧是同弧
∴∠ACE=∠CDE
∴△ACE∽△ADC
∴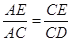 = tanD=
= tanD=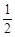
(3)先在△ACO中,设AE=x,
由勾股定理得
(x+3)²="(2x)" ²+3² ,解得x="2,"
∵∠BFO=90°=∠ACO
易证Rt△B0F∽Rt△BAC
得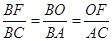 ,
,
设BO=y BF=z
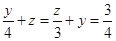
即4z=9+3y,4y=12+3z
解得z=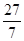 y=
y=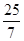
∴AB=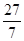 +4=
+4=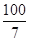
考点:圆的综合题.
【题型】解答题
【结束】
27
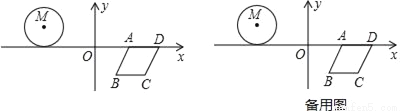
如图,⊙M与菱形ABCD在平面直角坐标系中,点M的坐标为(﹣3,1),点A的坐标为(2,0),点B的坐标为(1,﹣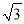 ),点D在x轴上,且点D在点A的右侧.
),点D在x轴上,且点D在点A的右侧.
(1)求菱形ABCD的周长;
(2)若⊙M沿x轴向右以每秒2个单位长度的速度平移,菱形ABCD沿x轴向左以每秒3个单位长度的速度平移,设菱形移动的时间为t(秒),当⊙M与AD相切,且切点为AD的中点时,连接AC,求t的值及∠MAC的度数;
(3)在(2)的条件下,当点M与AC所在的直线的距离为1时,求t的值.
科目:初中数学 来源:福建省建瓯市2018届九年级数学上册期末测试卷 题型:解答题
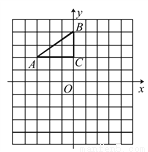
如图,在平面直角坐标系中,Rt△ABC的三个顶点分别是A(-3,2),B(0,4),C(0,2).
(1)将△ABC以点C为旋转中心旋转180°,画出旋转后对应的△A1B1C;平移△ABC,若点A的对应点A2的坐标为(0,-4),画出平移后对应的△A2B2C2;
(2)若将△A1B1C绕某一点旋转可以得到△A2B2C2,请直接写出旋转中心的坐标;
(3)在x轴上有一点P,使得PA+PB的值最小,请直接写出点P的坐标.
查看答案和解析>>
科目:初中数学 来源:2017年吉林省长春市中考数学模拟试卷 题型:单选题
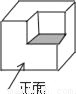
如图的几何体是由一个正方体切去一个小正方体形成的,它的主视图是( )
A.  B.
B.  C.
C.  D.
D. 
查看答案和解析>>
科目:初中数学 来源:2017-2018学年度第一学期海南省海口市七年级数学科期末检测模拟 题型:单选题
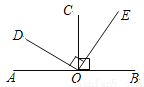
如图,CO⊥AB于点O,DO⊥EO,若∠DOC=58°40′,则∠BOE等于( )
A. 31°20′ B. 32°20′ C. 58°40′ D. 68°40′
C 【解析】∵DO⊥EO,CO⊥AB, ∴∠DOC+∠COE=90°, ∠BOE+∠COE=90°, ∴∠BOE=∠DOC=58°40′. 故选C.查看答案和解析>>
科目:初中数学 来源:2017-2018学年度第一学期海南省海口市七年级数学科期末检测模拟 题型:单选题
数据36000000用科学记数法表示为( )
A. 36×106 B. 3.6×106 C. 3.6×107 D. 3.6×108
C 【解析】36000000=3.6×107. 故选C.查看答案和解析>>
科目:初中数学 来源:江苏省苏州市2017年中考数学二模试卷 题型:解答题
“母亲节”前夕,某花店用4000元购进若干束花,很快售完,接着又用4500元购进第二批花,已知每束花的进价比第一批的进价少5元,且第二批所购花的束数是第一批所购花束数的1.5倍,求第一批花每束的进价是多少?
第一批花每束的进价是20元/束 【解析】试题分析:设第一批花每束的进价是x元/束,则第一批进的数量是: ,第二批进的数量是: ,再根据等量关系:第二批进的数量=第一批进的数量×1.5可得方程. 试题解析:设第一批花每束的价格为元, , 两边同时乘以得, , . ∴第一批花每束的进价为元.查看答案和解析>>
科目:初中数学 来源:江苏省苏州市2017年中考数学二模试卷 题型:填空题
若点(a,b)在一次函数y=2x﹣3上,则代数式3b﹣6a+1的值是________.
-8 【解析】把代入, 得, , ∴, ∴.查看答案和解析>>
科目:初中数学 来源:山东省德州市2018届九年级上期末模拟数学试卷 题型:解答题
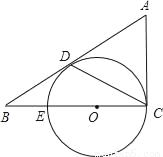
如图,△ABC中,∠ACB=90°,D是边AB上一点,且∠A=2∠DCB.E是BC边上的一点,以EC为直径的⊙O经过点D.
(1)求证:AB是⊙O的切线;
(2)若CD的弦心距为1,BE=EO,求BD的长.
查看答案和解析>>
科目:初中数学 来源:山东省德州市2018届九年级上期中数学试卷 题型:单选题
观察下列表格,一元二次方程x2﹣x﹣1.1=0的最精确的一个近似解是( )
x | 1.1 | 1.2 | 1.3 | 1.4 | 1.5 | 1.6 | 1.7 | 1.8 | 1.9 |
x2﹣x﹣1.1 | ﹣0.99 | ﹣0.86 | ﹣0.71 | ﹣0.54 | ﹣0.35 | ﹣0.14 | 0.09 | 0.34 | 0.61 |
A. 0.09 B. 1.1 C. 1.6 D. 1.7
D 【解析】根据图表数据找出一元二次方程最接近0的未知数的值,即为最精确的近似解. 【解析】 ∵x=1.7时,x2﹣x﹣1.1的值0.09最小, ∴一元二次方程x2﹣x﹣1.1=0的最精确的一个近似解是1.7. 故选D.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com