
整式-0.3x2y,0,  ,
, 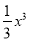 ,
, 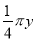 ,
, 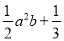 中,单项式的个数有( )
中,单项式的个数有( )
A. 3个 B. 4个 C. 5个 D. 6个
B 【解析】-0.3x2y是单项式;0是单项式; 是多项式; 是单项式; 是单项式; 是多项式,单项式共有4个, 故选B. 互动英语系列答案
互动英语系列答案 名牌学校分层周周测系列答案
名牌学校分层周周测系列答案科目:初中数学 来源:2017-2018学年北师大版八年级数学下册 期中测评 题型:解答题
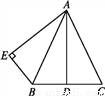
如图所示,AB=AC,点D是BC的中点,AB平分∠DAE,AE⊥BE,垂足为E.求证:AD=AE.
查看答案和解析>>
科目:初中数学 来源:四川省遂宁市2018届九年级上学期教学水平监测数学试卷 题型:单选题
如图,在正△ABC中,D,E分别在AC,AB上,且 ,AE=BE,则有
,AE=BE,则有
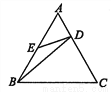
A. △AED∽△ABC B. △ADB∽△BED
C. △BCD∽△ABC D. △AED∽△CBD
D 【解析】试题分析:因为△ABC是正三角形,所以∠A=∠C=60°,可设AD=a,则AC=3a,而AB=AC=BC=3a,所以AE=BE=a,所以==,又==,所以=,∠A=∠C=60°,故△AED∽△CBD,故选:D.查看答案和解析>>
科目:初中数学 来源:重庆市校2017-2018学年七年级上学期第二阶段考试数学试卷 题型:解答题
计算:
(1)  ;
;
(2) 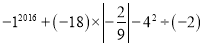 .
.
查看答案和解析>>
科目:初中数学 来源:重庆市校2017-2018学年七年级上学期第二阶段考试数学试卷 题型:单选题
如图,圆的周长为4个单位.在该圆的4等分点处分别标上0、1、2、3,先让圆周上表示数字0的点与数轴上表示-1的点重合,再将数轴按逆时针方向环绕在该圆上.则数轴上表示-2017的点与圆周上重合点的数字是( ) .
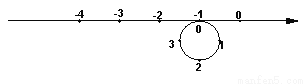
A. 0 B. 1 C. 2 D. 3
A 【解析】试题解析:由题意可得, (2017-1)÷4=2016÷4=504, 每四个为一个循环,每个循环对应圆圈上的点是3、2、1、0, ∴数轴上表示-2017的点与圆周上表示数字0重合, 故选A.查看答案和解析>>
科目:初中数学 来源:重庆市校2017-2018学年七年级上学期第二阶段考试数学试卷 题型:单选题
 的相反数是( )
的相反数是( )
A. 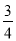 B.
B. 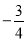 C.
C. 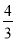 D.
D. 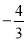
查看答案和解析>>
科目:初中数学 来源:2018春季学北师大版九年级数学下册期中测评试卷 题型:解答题
已知函数y=2x2+4x-3.
(1)通过配方,写出抛物线的开口方向、对称轴和顶点坐标;
(2)分别求出抛物线与x轴、y轴的交点坐标.
(1) 对称轴是直线x=-1,顶点坐标为(-1,-5);(2) 交点坐标为(0,-3). 【解析】试题分析:(1)根据的值可直接得到二次函数的开口方向,把二次函数化成顶点式即可写出顶点坐标、对称轴; (2)令二次函数中求出对应的的值,可得到二次函数图象与轴的交点坐标;令二次函数中求出对应的的值,可得到二次函数图象与轴的交点坐标; 试题解析: (1)y=2x2+4x-3=2(...查看答案和解析>>
科目:初中数学 来源:2018春季学北师大版九年级数学下册期中测评试卷 题型:单选题
如果∠A为锐角,且cos A≤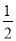 ,那么( )
,那么( )
A. 0°<∠A<60° B. 60°≤∠A<90° C. 0°<∠A≤30° D. 30°≤∠A<90°
B 【解析】试题解析:当∠A是锐角时,余弦值随角度的增大而减小. 故选B.查看答案和解析>>
科目:初中数学 来源:湖北省武汉市洪山区2018届九年级(上)期中数学试卷 题型:单选题
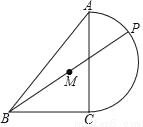
如图,在等腰Rt△ABC中,斜边AB=8,点P在以AC为直径的半圆上,M为PB的中点,当点P沿半圆从点A运动至点C时,点M运动的路径长是( )
A. 2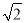 π B.
π B. 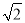 π C. 2π D. 2
π C. 2π D. 2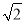
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com