练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    计算：

    (1)x(x＋3)(x＋5)；

    (2)(5x＋2y)(5x－2y)－5x(5x－3y)

    (1) x3＋8x2＋15x；(2)－4y2＋15xy 【解析】试题分析：（1）先算多项式乘多项式，再算单项式乘多项式； （2）先用平方差公式和单项式乘多项式法则计算，再合并同类项． 试题解析：【解析】 （1）原式= ； （2）原式==．
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源：北师大版七年级数学下册 第二章 相交线与平行线 2.1 两条直线的位置关系 同步训练题 题型：单选题

    如图，AD⊥BD，CD⊥BC，AB＝5cm，BC＝3cm，则线段BD的长度的取值范围是( )

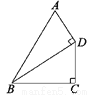
    A. 大于3cm B. 小于5cm C. 大于3cm且小于5cm D. 大于3cm或小于5cm

    C 【解析】试题解析：∵AD⊥BD，BC⊥CD，AB=5cm，BC=3cm， ∴BC＜BD＜AB， 即BD的长度的取值范围是大于3cm且小于5cm． 故选C．

    查看答案和解析>>

    科目：初中数学 来源：北师大版七年级数学下1.2幂的乘方与积的乘方 第1课时 幂的乘方 同步练习 题型：单选题

    9m·27n可以写为(　　)

    A. 9m+3n B. 27m+n C. 32m+3n D. 33m+2n

    C 【解析】原式= ，故选C.

    查看答案和解析>>

    科目：初中数学 来源：北师大版七年级数学下1.4.2 单项式与多项式相乘 同步练习 题型：解答题

    化简:

    (1)(-2ab)(3a2-2ab-4b2);

    (2)3x(2x-3y)-(2x-5y)·4x.

    (1) -6a3b+4a2b2+8ab3；(2) -2x2+11xy. 【解析】试题分析：（1）根据单项式乘多项式法则计算即可； （2）先用单项式乘多项式法则计算，然后合并同类项即可． 试题解析：【解析】 (1)原式=－6a3b+4a2b2+8ab3； (2)原式=6x2-9xy-8x2+20xy=－2x2+11xy．

    查看答案和解析>>

    科目：初中数学 来源：北师大版七年级数学下1.4.2 单项式与多项式相乘 同步练习 题型：单选题

    -5x·(2x2-x+3)的计算结果为(　　)

    A. -10x3+5x2-15x B. -10x3-5x2+15x C. 10x3-5x2-15x D. -10x3+5x2-3

    A 【解析】【解析】 原式=．故选A．

    查看答案和解析>>

    科目：初中数学 来源：北师大版 七年级数学下册 第一章　整式的乘除 1.4 整式的乘法 多项式与多项式相乘 同步课时练习题 题型：单选题

    下列计算中，结果为x2＋5x－6的算式是( )

    A. (x＋2)(x＋3) B. (x＋2)(x－3)

    C. (x＋6)(x－1) D. (x－2)(x－3)

    C 【解析】解：A． (x＋2)(x＋3) =x2+5x+6； B． (x＋2)(x－3)=x2-x-6； C． (x＋6)(x－1)=x2+5x-6； D． (x－2)(x－3)=x2-5x+6． 故选C．

    查看答案和解析>>

    科目：初中数学 来源：北师大版九年级上册数学全册综合测试卷一 题型：解答题

    如图，△ABC中，EF∥BC，FD∥AB，AE=12，BE=18，AF=14，CD=24，求线段FC，EF的长．

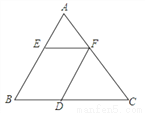
    21. 【解析】试题分析：由EF∥BC，FD∥AB，可以得到△AEF∽△ABC∽△FDC,根据相似三角形的对应边成比例,即可求出线段EF和FC的长. 【解析】 ∵EF∥BC，FD∥AB， ∴四边形EBDF是平行四边形， ∴EF=BD，DF=BE=18， 设EF=x， ∵EF∥BC，FD∥AB， ∴△AEF∽△ABC∽△FDC， ∴ ，即 ， ...

    查看答案和解析>>

    科目：初中数学 来源：北师大版九年级上册数学全册综合测试卷一 题型：单选题

    解一元二次方程x（x+3）=x得到它的根是（　　）

    A. x=﹣3 B. x1=0或x2=﹣3 C. x=﹣2 D. x1=0或x2=﹣2

    D 【解析】∵x（x+3）=x, ∴x（x+3）-x=0, ∴x（x+2）=0, ∴x1=0或x2=﹣2 故选D.

    查看答案和解析>>

    科目：初中数学 来源：2017-2018学年九年级数学人教版上册：第21章 一元二次方程 单元测试卷 题型：解答题

    已知关于x的方程3x2－(a－3)x－a＝0(a>0)．

    (1)求证：方程总有两个不相等的实数根；

    (2)若方程有一个根大于2，求a的取值范围．

    (1)证明见解析；（2）a>6. 【解析】试题分析：（1）先计算根的判别式得到△=（a＋3）2，然后根据a>0得到△＞0，则可根据判别式的意义得到结论； （2）利用公式法求得方程的两个解为x1＝－1，x2＝，再由方程有一个根大于2，列出不等式，解不等式即可求得a的取值． 试题解析： （1）证明：Δ＝（a－3）2－4×3×（－a）＝（a＋3）2. ∵a>0， ∴（...

    查看答案和解析>>

    同步练习册答案