
如图,将△ABC绕着点C顺时针旋转50°后得到△A’B’C.若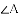
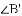
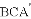 的度数为( )
的度数为( )
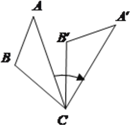
A. 30° B. 50° C. 80° D. 90°
科目:初中数学 来源:福建省2016-2017学年七年级下学期第二次月考数学试卷 题型:填空题
如图,为了测量小池塘两旁A,B两点之间的距离而构造的三角形,经测量知AO=CO,∠B=∠D,为了使CD和AB的长度相等,只需再加一个条件________________.(不添加其它字母和辅助线)

查看答案和解析>>
科目:初中数学 来源:福建省泉州市2017-2018学年七年级下期末质量检测数学试卷 题型:解答题
阅读下列材料:
我们知道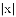 的几何意义是在数轴上数
的几何意义是在数轴上数
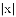 =
=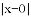 ,也就是说,
,也就是说,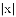 表示在数轴上数
表示在数轴上数
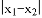 表示在数轴上数
表示在数轴上数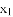 与数
与数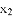 对应的点之间的距离;
对应的点之间的距离;
例1.解方程|
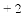

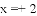
例2.解不等式|








例3.解方程|











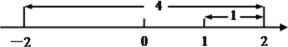
参考阅读材料,解答下列问题:
(1)方程|
(2)解不等式:|
(3)解不等式:|

查看答案和解析>>
科目:初中数学 来源:福建省泉州市2017-2018学年七年级下期末质量检测数学试卷 题型:填空题
如图,长方形ABCD中,AB=4,AD=2.点Q与点P同时从点A出发,点Q以每秒1个单位的速度沿A→D→C→B的方向运动,点P以每秒3个单位的速度沿A→B→C→D的方向运动,当P,Q两点相遇时,它们同时停止运动.设Q点运动的时间为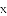
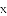
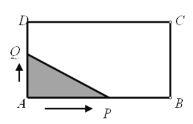
查看答案和解析>>
科目:初中数学 来源:福建省泉州市2017-2018学年七年级下期末质量检测数学试卷 题型:单选题
在△ABC中,∠A∶∠B∶∠C=1∶2∶3,则△ABC的形状是
A. 等腰三角形 B. 直角三角形 C. 等边三角形 D. 等腰直角三角形
查看答案和解析>>
科目:初中数学 来源:贵州省铜仁市2018年中考数学试卷 题型:解答题
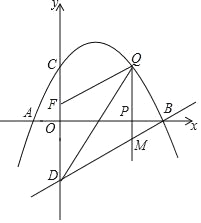
如图,已知抛物线经过点A(﹣1,0),B(4,0),C(0,2)三点,点D与点C关于x轴对称,点P是x轴上的一个动点,设点P的坐标为(m,0),过点P做x轴的垂线l交抛物线于点Q,交直线BD于点M.
(1)求该抛物线所表示的二次函数的表达式;
(2)已知点F(0, ),当点P在x轴上运动时,试求m为何值时,四边形DMQF是平行四边形?
),当点P在x轴上运动时,试求m为何值时,四边形DMQF是平行四边形?
(3)点P在线段AB运动过程中,是否存在点Q,使得以点B、Q、M为顶点的三角形与△BOD相似?若存在,求出点Q的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源:贵州省铜仁市2018年中考数学试卷 题型:单选题
在同一平面内,设a、b、c是三条互相平行的直线,已知a与b的距离为4cm,b与c的距离为1cm,则a与c的距离为( )
A. 1cm B. 3cm C. 5cm或3cm D. 1cm或3cm
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com