
分解因式ma2﹣2mab+mb2=_____.
m(a﹣b)2 【解析】ma2﹣2mab+mb2=m(a2﹣2ab+b2)=m(a-b)2. 故答案为m(a-b)2.科目:初中数学 来源:湖南省2017-2018学年八年级数学上期末复习检测数学试卷 题型:填空题
一次函数y=kx+2,当x=3时,y=﹣7,则k的值等于________;当x=________时,y=5.
﹣3 ﹣1. 【解析】把x=3时,y=?7代入y=kx+2,得 ?7=3k+2, 解得k=?3; 所以y=?3x+2, 把y=5代入得,5=?3x+2, 解得x=?1, 所以当x=?1时,y=5; 故答案为?3;?1.查看答案和解析>>
科目:初中数学 来源:2017年安徽省六安市金安区滨河学校中考数学模拟试卷 题型:解答题
解方程:3x2﹣7x+4=0.
x1=,x2=1. 【解析】试题分析:直接利用因式分解法解方程即可. 试题解析: 分解因式得:(3x﹣4)(x﹣1)=0, 可得3x﹣4=0或x﹣1=0, 解得:x1=,x2=1.查看答案和解析>>
科目:初中数学 来源:2017年湖北省随州市中考数学模拟试卷 题型:解答题
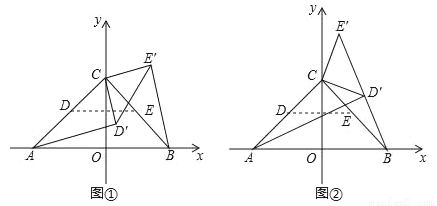
在平面直角坐标系中,点 A(﹣2,0),B(2,0),C(0,2),点 D,点E分别是 AC,BC的中点,将△CDE绕点C逆时针旋转得到△CD′E′,及旋转角为α,连接 AD′,BE′.
(1)如图①,若 0°<α<90°,当 AD′∥CE′时,求α的大小;
(2)如图②,若 90°<α<180°,当点 D′落在线段 BE′上时,求 sin∠CBE′的值;
(3)若直线AD′与直线BE′相交于点P,求点P的横坐标m的取值范围(直接写出结果即可).
查看答案和解析>>
科目:初中数学 来源:2017年湖北省随州市中考数学模拟试卷 题型:填空题
(3分)一个足球被从地面向上踢出,它距地面的高度h(m)与足球被踢出后经过的时间t(s)之间具有函数关系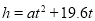 ,已知足球被踢出后经过4s落地,则足球距地面的最大高度是 m.
,已知足球被踢出后经过4s落地,则足球距地面的最大高度是 m.
查看答案和解析>>
科目:初中数学 来源:2017年湖北省随州市中考数学模拟试卷 题型:单选题
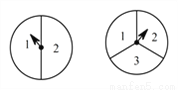
如图,现分别旋转两个标准的转盘,两个转盘分别被分成两等分和三等分,则转盘所转到的两个数字之积为奇数的概率是( )
A. 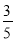 B.
B. 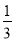 C.
C. 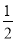 D.
D. 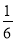
查看答案和解析>>
科目:初中数学 来源:2017年天津九中中考数学冲刺试卷 题型:解答题
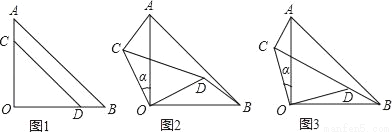
两块等腰直角三角形纸片AOB和COD按图1所示放置,直角顶点重合在点O处,AB=25,CD=17.保持纸片AOB不动,将纸片COD绕点O逆时针旋转α(0°<α<90°)角度,如图2所示.
(1)利用图2证明AC=BD且AC⊥BD;
(2)当BD与CD在同一直线上(如图3)时,求AC的长和α的正弦值.
查看答案和解析>>
科目:初中数学 来源:2017年天津九中中考数学冲刺试卷 题型:单选题
如图,已知在△ABC中,CD是AB边上的高线,BE平分∠ABC,交CD于点E,BC=5,DE=2,则△BCE的面积等于( )
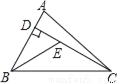
A. 10 B. 7 C. 5 D. 4
C 【解析】作EF⊥BC于F, ∵BE平分∠ABC,ED⊥AB,EF⊥BC, ∴EF=DE=2, ∴S△BCE=BC?EF=×5×2=5, 故选C.查看答案和解析>>
科目:初中数学 来源:2017-2018学年江苏省苏州市初二上期中试卷数学试卷 题型:解答题
实验与探究:
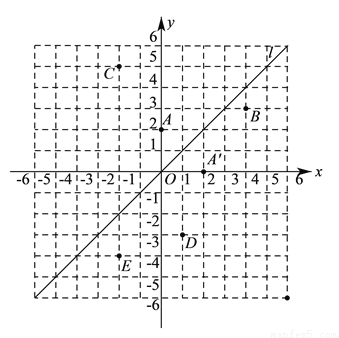
( )如图,直线
)如图,直线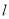 为第一、三象限的角平分线,观察易知
为第一、三象限的角平分线,观察易知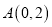 关于直线
关于直线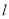 的对称点
的对称点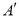 的坐标为
的坐标为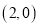 ,请在图中分别标明
,请在图中分别标明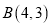 、
、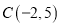 关于直线
关于直线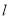 的对称点
的对称点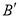 、
、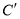 的位置,并写出他们的坐标:
的位置,并写出他们的坐标: 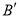 __________、
__________、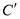 __________.
__________.
(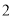 )结合图形观察以上三组点的坐标,你会发现:坐标平面内任一点
)结合图形观察以上三组点的坐标,你会发现:坐标平面内任一点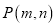 关于第一、三象限的角平分线
关于第一、三象限的角平分线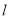 的对称点
的对称点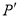 的坐标为__________ (不必证明).
的坐标为__________ (不必证明).
(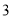 )已知两点
)已知两点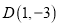 、
、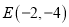 ,在直线
,在直线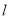 上是否存在一点
上是否存在一点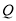 ,使点
,使点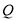 到
到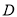 、
、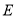 两点的距离之和最小,并求出最小距离.
两点的距离之和最小,并求出最小距离.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com