
 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源:黑龙江省哈尔滨市2017-2018学年八年级上学期期末考试数学试卷 题型:解答题
先化简,再求值: 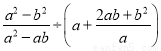 ,其中
,其中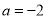 ,
, 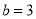 .
.
查看答案和解析>>
科目:初中数学 来源:江苏省东部分校2017-2018学年七年级上学期期末考试数学试卷 题型:单选题
观察下列等式:
第一层 1+2=3
第二层 4+5+6=7+8
第三层 9+10+11+12=13+14+15
第四层 16+17+18+19+20=21+22+23+24
……
在上述的数字宝塔中,从上往下数,2018在第( )层.
A. 43 B. 44 C. 45 D. 46
B 【解析】【解析】 第一层:第一个数为12=1,最后一个数为22﹣1=3,第二层:第一个数为22=4,最后一个数为32﹣1=8,第三层:第一个数为32=9,最后一个数为42﹣1=15,∵442=1936,452=2025,又∵1936<2018<2025,∴在上述数字宝塔中,从上往下数,2018在第44层,故答案为:44.查看答案和解析>>
科目:初中数学 来源:浙江杭州富阳2016-2017学年八年级上学期期末数学试卷 题型:填空题
如图所示, 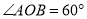 ,
, 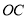 平分
平分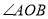 ,如果射线
,如果射线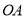 上的点
上的点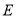 满足
满足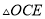 是等腰三角形,那么
是等腰三角形,那么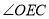 的度数为__________.
的度数为__________.
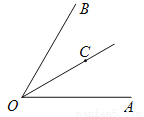
查看答案和解析>>
科目:初中数学 来源:浙江杭州富阳2016-2017学年八年级上学期期末数学试卷 题型:单选题
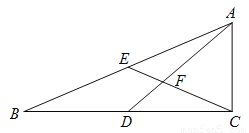
如图所示,在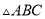 中,
中, 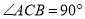 ,点
,点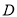 在
在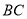 上,
上, 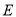 是
是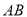 的中点,
的中点, 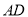 与
与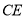 交于点
交于点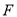 ,且
,且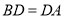 ,若
,若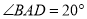 ,则
,则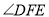 等于( )
等于( )
A. 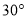 B.
B. 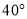 C.
C. 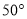 D.
D. 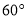
查看答案和解析>>
科目:初中数学 来源:江苏省泰兴市2017-2018学年八年级上学期期末考试数学试卷 题型:解答题
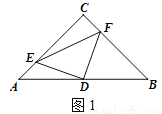
如图,△ABC中,AC=BC,∠C=90°,点D是AB的中点.
(1)如图1,若点E、F分别是AC、BC上的点,且AE=CF,请判别△DEF的形状,并说明理由;
(2)若点E、F分别是CA、BC延长线上的点,且AE=CF,则(1)中的结论是否仍然成立?请
说明理由.
查看答案和解析>>
科目:初中数学 来源:江苏省泰兴市2017-2018学年八年级上学期期末考试数学试卷 题型:填空题
△ABC是等腰三角形,腰上的高为8cm,面积为40cm2,则该三角形的周长是_______cm.
或. 【解析】(1)如图1,在△ABC中,AB=AC,∠A是锐角,BD是AC边上的高, 由题意可知:BD=8cm,S△ABC=BD·AC=40cm2, ∴AC=10cm=BC, ∴在Rt△ABD中,由勾股定理可得:AD=(cm), ∴DC=AC-AD=4cm, ∴在Rt△BDC中,由勾股定理可得:BC=(cm), ∴此时△ABC的周长=AB+AC+BC=(...查看答案和解析>>
科目:初中数学 来源:北师大版八年级数学上册 第七章 平行线的证明 单元测试 题型:解答题
已知:如图,E、F是平行四边行ABCD的对角线AC上的 两点,AE=CF。
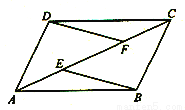
求证:(1)△ADF≌△CBE
(2)EB∥DF.
∵四边形ABCD为平行四边形, ∴AD∥BC,AD=BC. ………………(1分) ∴∠DAC=∠BCE. 又∵AE=CF,∴AF=CE ∴△ADF≌△CBE.……………………(4分) ∴∠AFD=∠CEB. ∴BE∥DF. ……………………………(6分 【解析】试题分析:要证△ADF≌△CBE,因为AE=CF,则两边同时加上EF,得到AF=CE,又因为AB...查看答案和解析>>
科目:初中数学 来源:四川省宜宾市2017-2018学年上学期期末教学质量监测八年级数学试卷 题型:单选题
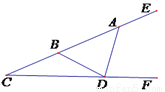
如图,在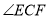 的两边上有点
的两边上有点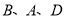 ,
, 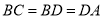 ,且
,且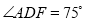 ,则
,则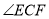 的度数为( )
的度数为( )
A. 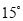 B.
B. 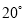 C.
C. 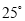 D.
D. 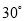
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com